Изобарная теплоёмкость

Определение

Удельная теплоемкость вещества, обычно обозначаемая как c{ displaystyle c}, — теплоемкость C{ displaystyle C} образца вещества, деленного на массу M{ displaystyle M} образца:

c=CM=1M⋅dQdТ{ displaystyle c = { frac {C} {M}} = { frac {1} {M}} cdot { frac { mathrm {d} Q} { mathrm {d} T}}}

куда dQ{ displaystyle mathrm {d} Q} представляет количество тепла, необходимое для равномерного повышения температуры образца с небольшим шагом dТ{ displaystyle mathrm {d} T}.

Как и теплоемкость объекта, удельная теплоемкость вещества может варьироваться, иногда существенно, в зависимости от начальной температуры. Т{ displaystyle T} образца и давление п{ displaystyle p} применяется к нему. Следовательно, ее следует рассматривать как функцию c(п,Т){ displaystyle c (p, T)} этих двух переменных.

Эти параметры обычно указываются при указании удельной теплоемкости вещества. Например, «Вода (жидкость): cп{ displaystyle c_ {p}} = 4185,5 Дж / К / кг (15 ° C, 101,325 кПа) » Если не указано иное, опубликованные значения удельной теплоемкости c{ displaystyle c} как правило, действительны для некоторых стандартные условия по температуре и давлению.

Однако зависимость c{ displaystyle c} на начальную температуру и давление часто можно игнорировать в практических контекстах, например при работе в узких диапазонах этих переменных. В этих контекстах обычно опускают квалификатор (п,Т){ displaystyle (p, T)}, и аппроксимирует теплоемкость константой c{ displaystyle c} подходит для этих диапазонов.

Удельная теплоемкость — это интенсивное свойство вещества, внутренняя характеристика, которая не зависит от размера или формы рассматриваемого количества. (Квалификатор «специфический» перед экстенсивным свойством часто указывает на интенсивное свойство, производное от него.)

Вариации

Введение тепловой энергии в вещество, помимо повышения его температуры, обычно вызывает увеличение его объема и / или давления, в зависимости от того, как удерживается образец. Выбор последнего влияет на измеренную удельную теплоемкость даже при том же начальном давлении. п{ displaystyle p} и начальная температура Т{ displaystyle T}. Широко используются два конкретных варианта:

• Если давление поддерживается постоянным (например, при атмосферном давлении окружающей среды), а образец расширяется, расширение вызывает работай поскольку сила давления смещает корпус или окружающую жидкость. Эта работа должна производиться за счет поставляемой тепловой энергии. Полученная таким образом удельная теплоемкость называется измеренной. при постоянном давлении (или же изобарический), и часто обозначается cп{ displaystyle c_ {p}}, cп{ displaystyle c _ { mathrm {p}}}, так далее.
• С другой стороны, если расширение предотвращается — например, за счет достаточно жесткого корпуса или увеличения внешнего давления, чтобы противодействовать внутреннему, — работа не создается, и тепловая энергия, которая пошла бы в него, должна вместо этого способствовать внутренняя энергия образца, в том числе повышение его температуры на дополнительную величину. Полученная таким образом удельная теплоемкость называется измеренной. при постоянной громкости (или же изохорный) и обозначили cV{ displaystyle c_ {V}}, cv{ displaystyle c_ {v}} cv{ displaystyle c _ { mathrm {v}}}, так далее.

Значение cV{ displaystyle c_ {V}} обычно меньше, чем значение cп{ displaystyle c_ {p}}. Эта разница особенно заметна для газов, где значения при постоянном давлении обычно на 30–66,7% больше, чем при постоянном объеме. Следовательно коэффициент теплоемкости газов обычно составляет от 1,3 до 1,67.

Применимость

Удельную теплоемкость можно определить и измерить для газов, жидкостей и твердых тел довольно общего состава и молекулярной структуры. К ним относятся газовые смеси, растворы и сплавы или гетерогенные материалы, такие как молоко, песок, гранит и бетон, если рассматривать их в достаточно большом масштабе.

Удельная теплоемкость также может быть определена для материалов, которые изменяют состояние или состав при изменении температуры и давления, если изменения обратимы и постепенны. Таким образом, например, концепции могут быть определены для газа или жидкости, которые диссоциируют при повышении температуры, до тех пор, пока продукты диссоциации быстро и полностью рекомбинируют при падении.

Удельная теплоемкость не имеет значения, если вещество претерпевает необратимые химические изменения или если есть изменение фазы, например, плавление или кипение при резкой температуре в диапазоне температур, охватываемых измерением.

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

, (4.2)

где
m – масса, µ – молярная масса вещества,– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:

.

Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

.

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

.

Выразим
из негои подставим в формулу (4.10):

.

Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:

.

Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

.

Прологарифмируем
это выражение:

.

Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:

.

Откуда:

. (4.14)

Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.

Теплоёмкость для различных процессов и состояний вещества

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Теплоёмкость идеального газа

Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.

Молярная теплоёмкость при постоянном объёме:

CV=dUdT=i2R,{\displaystyle C_{V}={dU \over dT}={\frac {i}{2}}R,}

где R{\displaystyle R} ≈ 8,31 Дж/(моль·К) — универсальная газовая постоянная, i{\displaystyle i} — число .

Молярная теплоёмкость при постоянном давлении связана с CV{\displaystyle C_{V}} соотношением Майера:

CP=CV+R=i+22R.{\displaystyle C_{P}=C_{V}+R={{i+2} \over 2}R.}

Теплоёмкость кристаллов

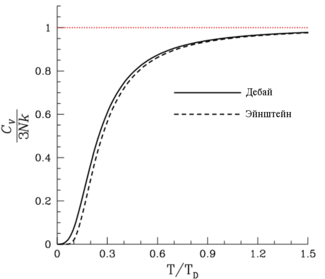
Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела

Существует несколько теорий теплоёмкости твердого тела:

• Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).
• Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.
• Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.

Воздух — идеальный газ

Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.

Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.

Удельная и молярная теплоёмкость

Молярная теплоёмкость — теплоёмкость 1 моля вещества :

CM=Cν=1νδQΔT,{\displaystyle C_{M}={\frac {C}{\nu }}={\frac {1}{\nu }}{\frac {\delta Q}{\Delta T}},}

где ν=mM,{\displaystyle \nu =m/M,} m{\displaystyle m} — масса, M{\displaystyle M} — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К).

Формула расчёта удельной теплоёмкости:

c=CMM=δQmdT,{\displaystyle c={\frac {C_{M}}{M}}={\frac {\delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

Теплоотдача и терморегуляция

Количество
теплоты Q,
переносимое вследствие теплопро­водности
за время Δt,
определяется формулой

Q=k₁ΔTΔSΔt/Δx

где
k₁—
коэффициент теплопроводности; ΔT/Δx
— градиент тем-

пературы
в направлении, перпендикулярном площадке
ΔS.

Количество
теплоты Q,
переносимое вследствие конвекции за
время Δt,
определяется формулой;

Q=k₂(T-T)ΔSΔt

где
k₂
— коэффициент теплопередачи при
конвекции; Т и Т
— соответственно
температуры поверхности ΔS
и омываемой среды.

Количество
теплоты Q,
излучаемое за время Δt
абсолютно черным телом, определяется
формулой (закон Стефана — Больцмана)

Q=σT4ΔSΔt

где
σ—
постоянная Стефана — Больцмана; Т
— абсолютная температура
тела; ΔS
— площадь излучающей поверхности тела.
Для
реальных физических тел закон Стефана
— Больцмана имеет
вид

Q=k₃σT4ΔSΔt

где
k₃
— коэффициент, учитывающий, что свойства
поверхности реальных
физических тел отличны от свойств
поверхности абсолютно
черного тела (k₃<. k>3=
1.

При
наличии двух встречных потоков радиации
от излу­чающей
поверхности к среде и от среды к
поверхности закон Стефана
— Больцмана имеет вид

Q=k₃σ(T4–T4)ΔSΔt

где
Т и Т
— абсолютные температуры тела и
среды; ΔS
— площадь
излучающей поверхности тела.

Длина
волны λ_т,
которой соответствует максимум
излуча-тельной способности черного
тела, обратно пропорциональна абсолютной
температуре Т (закон смещения Вина):

λ_m=b/T

где
b
— постоянная закона смещения Вина.

Теплоемкость и ее виды

Согласно физическому определению, теплоемкость — это величина, показывающая, сколько нужно на систему затратить теплоты, чтобы ее нагреть на 1 градус Цельсия или на 1 кельвин. Поскольку процессы нагревания и охлаждения являются обратимыми, то при охлаждении системы на 1 градус выделяется количество теплоты, равное ее теплоемкости.

Как физическая величина теплоемкость может быть абсолютной, молярной или массовой. Определение абсолютной теплоемкости для произвольной системы было дано выше. Молярной называется теплоемкость на 1 моль газа, массовой — на 1 кг газа. Молярная величина чаще используется для рассматриваемого агрегатного состояния материи.

В зависимости от изопроцесса, при котором измеряют теплоемкость, она бывает изохорной и изобарной. В первом случае в системе с газом не изменяется объем, во втором случае сохраняется давление.

Литература

• Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
•  (недоступная ссылка)
•  (недоступная ссылка)
•  (недоступная ссылка)
• Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
•  (недоступная ссылка)
• Лифшиц Е. М. // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 77–78.
• Лифшиц Е. М. // Большая советская энциклопедия / Ред. А. М. Прохоров. — 3-е издание. — М.: Большая Советская Энциклопедия, 1976. — Т. 25. — С. 451.
• Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2006. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
• // Большая российская энциклопедия. — М.: Большая российская энциклопедия, 2016. — Т. 32. — С. 54.

Физическая основа теплоемкости

Температура образца вещества отражает среднее значение кинетическая энергия составляющих его частиц (атомов или молекул) относительно его центра масс. Однако не вся энергия, передаваемая образцу вещества, идет на повышение его температуры, примером чего является теорема о равнораспределении.

Одноатомные газы

Квантовая механика предсказывает, что при комнатной температуре и обычном давлении изолированный атом в газе не может хранить какое-либо значительное количество энергии, кроме как в форме кинетической энергии. Таким образом, теплоемкость на моль одинаково для всех одноатомных газов (например, благородных газов). Точнее, cV,м=3р2≈{ Displaystyle c_ {V, mathrm {m}} = 3R / 2 приблизительно {}}12,5 Дж / К / моль и cп,м=5р2≈{ Displaystyle c_ {P, mathrm {m}} = 5R / 2 приблизительно {}}21 Дж / К / моль, где р≈{ Displaystyle R приблизительно {}}8,31446 Дж / К / моль — это установка идеального газа (который является продуктом Постоянная преобразования Больцмана из кельвин микроскопическая единица энергии к макроскопической единице энергии джоуль, и Число Авогадро).

Следовательно, удельная теплоемкость (на единицу массы, а не на моль) одноатомного газа будет обратно пропорциональна его (размерной) атомный вес А{ displaystyle A}. То есть примерно

cV≈{ displaystyle c_ {V} приблизительно {}}12470 Дж / К / кгАcп≈{ displaystyle / A quad quad quad c_ {p} приблизительно {}}20785 Дж / К / кгА{ displaystyle / A}

Для благородных газов, от гелия до ксенона, эти расчетные значения равны

Газ	Он	Ne	Ar	Kr	Xe
А{ displaystyle A}	4.00	20.17	39.95	83.80	131.29
cV{ displaystyle c_ {V}} (Дж / К / м3)	3118	618.3	312.2	148.8	94.99
cп{ displaystyle c_ {p}} (Дж / К / кг)	5197	1031	520.3	248.0	158.3

Многоатомные газы

С другой стороны, многоатомная молекула газа (состоящая из двух или более связанных вместе атомов) может накапливать тепловую энергию в других формах, помимо своей кинетической энергии. Эти формы включают вращение молекулы и колебание атомов относительно ее центра масс.

Эти дополнительные степени свободы или «режимы» вносят вклад в удельную теплоемкость вещества. А именно, когда в газ с многоатомными молекулами вводится тепловая энергия, только часть ее идет на увеличение их кинетической энергии и, следовательно, температуры; остальное перейдет в те другие степени свободы. Чтобы достичь такого же повышения температуры, моль этого вещества должен быть передан большей тепловой энергии, чем моль одноатомного газа. Следовательно, теплоемкость многоатомного газа зависит не только от его молекулярной массы, но и от числа степеней свободы, которые имеют молекулы.

Квантовая механика далее утверждает, что каждая вращательная или колебательная мода может забирать или терять энергию только в определенном дискретном количестве (квантах). В зависимости от температуры, средняя тепловая энергия на молекулу может быть слишком маленькой по сравнению с квантами, необходимыми для активации некоторых из этих степеней свободы. Эти режимы называются «замороженными». В этом случае удельная теплоемкость вещества будет увеличиваться с температурой, иногда ступенчато, по мере того, как больше режимов размораживаются и начинают поглощать часть подводимой тепловой энергии.

Например, молярная теплоемкость азот N₂ при постоянной громкости cV,м={ displaystyle c_ {V, mathrm {m}} = {}} 20,6 Дж / К / моль (при 15 ° C, 1 атм), что составляет 2,49р{ displaystyle R}. Это значение, ожидаемое из теории, если каждая молекула имеет 5 степеней свободы. Оказывается, это три градуса вектора скорости молекулы плюс два градуса ее вращения вокруг оси, проходящей через центр масс и перпендикулярной линии двух атомов. Из-за этих двух дополнительных степеней свободы удельная теплоемкость cV{ displaystyle c_ {V}} из N₂ (736 Дж / К / кг) в 5/3 раза больше, чем у гипотетического одноатомного газа с той же молекулярной массой 28 (445 Дж / К / кг).

Это значение удельной теплоемкости азота практически постоянно от -150 ° C до примерно 300 ° C. В этом температурном диапазоне две дополнительные степени свободы, соответствующие колебаниям атомов, растяжению и сжатию связи, все еще «заморожены». Примерно при этой температуре эти режимы начинают «размораживаться», и в результате cV{ displaystyle c_ {V}} сначала начинает быстро увеличиваться, затем медленнее по мере приближения к другому постоянному значению. Оно составляет 35,5 Дж / К / моль при 1500 ° C, 36,9 при 2500 ° C и 37,5 при 3500 ° C. Последнее значение почти точно соответствует предсказанному значению для 7 степеней свободы на молекулу.

Воздух — идеальный газ

Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.

Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.

Виды теплопередачи

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Если мы греемся у камина, то получаем тепло конвекцией или излучением?

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Удельная и молярная теплоёмкость

Молярная теплоёмкость — теплоёмкость 1 моля вещества :

CM=Cν=1νδQΔT,{\displaystyle C_{M}={\frac {C}{\nu }}={\frac {1}{\nu }}{\frac {\delta Q}{\Delta T}},}

где ν=mM,{\displaystyle \nu =m/M,} m{\displaystyle m} — масса, M{\displaystyle M} — молярная масса вещества.

Теплоёмкость единичной массы вещества называется удельной теплоёмкостью и, в системе СИ, измеряется в Дж/(кг·К).

Формула расчёта удельной теплоёмкости:

c=CMM=δQmdT,{\displaystyle c={\frac {C_{M}}{M}}={\frac {\delta Q}{mdT}},}

где c — удельная теплоёмкость, m — масса нагреваемого (охлаждающегося) вещества.

Теплоёмкость идеального газа в изопроцессах

Адиабатический

В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть dQ={\displaystyle dQ=0}. Однако, объём, давление и температура меняются, то есть dT≠{\displaystyle dT\neq 0}.

Следовательно, теплоёмкость идеального газа в адиабатическом процессе равна нулю: C=dT={\displaystyle C={0 \over dT}=0}.

Изотермический

В изотермическом процессе постоянна температура, то есть dT={\displaystyle dT=0}. При изменении объёма газу передаётся (или отбирается) некоторое количество тепла. Следовательно, теплоёмкость идеального газа равна плюс-минус бесконечности: C→±∞{\displaystyle C\to \pm \infty }

Изохорный

В изохорном процессе постоянен объём, то есть δV={\displaystyle \delta V=0} и, следовательно газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид:

dU=δQ=νCVdT.(1){\displaystyle dU=\delta Q=\nu C_{V}dT.\qquad (1)}

А для идеального газа

dU=i2νRΔT.{\displaystyle dU={\frac {i}{2}}\nu R\Delta T.}

Таким образом,

CV=i2R,{\displaystyle C_{V}={\frac {i}{2}}R,}

где i{\displaystyle i} — число частиц газа.

Другая формула:

CV=Rγ−1,{\displaystyle C_{V}={\frac {R}{\gamma -1}},}

где γ{\displaystyle \gamma } — показатель адиабаты, R{\displaystyle R} — газовая постоянная газа.

Изобарный

Молярная теплоёмкость при постоянном давлении обозначается как Cp{\displaystyle C_{p}}. В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера Cp=Cv+R{\displaystyle C_{p}=C_{v}+R}.
Уравнение Майера вытекает из первого начала термодинамики:

δQ=dU+δA,(2){\displaystyle \delta Q=\mathrm {d} U+\delta A,\qquad (2)}.

В рассматриваемом случае, согласно определению теплоёмкости:

δQ=CpdT,{\displaystyle \delta Q=C_{p}\mathrm {d} T,}

Учитываем, что работа газа равна :

δA=d(pV)=nRdT=pdV+Vdp=pdV,(Vdp=)(3){\displaystyle \delta A=\mathrm {d} (pV)=nR\mathrm {d} T\qquad =p\mathrm {d} V\qquad +V\mathrm {d} p\qquad =p\mathrm {d} V\qquad ,(V\mathrm {d} p\qquad =0)(3)}

Согласно уравнению Менделеева-Клапейрона для одного моля газа:

pdV=RdT.(4){\displaystyle p\mathrm {d} V=R\mathrm {d} T.\qquad (4)}

Подставляя уравнение (4) в (3) получаем:

δA=RdT(5){\displaystyle \delta A=R\mathrm {d} T\qquad (5)}

Так как энергия одной молекулы равна <e>=i2kT{\displaystyle <e>={\frac {i}{2}}kT} (6), то и внутренняя энергия в целом и при изобарном процессе будет определяться по соотношению (1). Следовательно, подставляя уравнения (1) и (5) в (2) получаем соотношение Майера.

Молекулярно-кинетическая теория позволяет вычислить значения молярной теплоёмкости для классического идеального газа газов через значение универсальной газовой постоянной исходя из уравнения (6) и предположения, что молекулы газа не взаимодействуют между собой:

• для общего случая Cp=i+22R,{\displaystyle C_{p}={\frac {i+2}{2}}R,}
• для одноатомных газов Cp=52R,{\displaystyle C_{p}={\frac {5}{2}}R,} то есть около 20.8 Дж/(моль·К);
• для двухатомных газов и многоатомных газов с линейными молекуламиCp=72R,{\displaystyle C_{p}={\frac {7}{2}}R,} то есть около 29.1 Дж/(моль·К);
• для многоатомных газов с нелинейными молекуламиCp=4R,{\displaystyle C_{p}=4R,} то есть около 33.3 Дж/(моль·К).

Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).

Теплоёмкость реального газа может значительно отклонятся от теплоёмкости идеального газа. Так при температуре в 25 °С и атмосферном давлении атомарный водород имеет теплоёмкость 2,50R , а атомарный кислород — 2,63R. Также теплоёмкость реального газа зависит от температуры.

Удельная, молярная и объёмная теплоёмкости

Очевидно, что чем больше масса тела, тем больше требуется теплоты для его нагревания, и теплоёмкость тела пропорциональна количеству вещества, содержащегося в нём. Количество вещества может характеризоваться массой или количеством молей. Поэтому удобно пользоваться понятиями удельной теплоёмкости (теплоёмкости единицы массы тела):

c=Cm{\displaystyle c={C \over m}}

и молярной теплоёмкости (теплоёмкости одного моля вещества):

Cμ=Cν,{\displaystyle C_{\mu }={C \over \nu },}

где ν=mμ{\displaystyle \nu ={m \over \mu }} — количество вещества в теле; m{\displaystyle m} — масса тела; μ{\displaystyle \mu } — молярная масса. Молярная и удельная теплоёмкости связаны соотношением Cμ=cμ{\displaystyle C_{\mu }=c\mu }.

Объёмная теплоёмкость (теплоёмкость единицы объёма тела):

C′=CV.{\displaystyle C’={C \over V}.}

Изохорная теплоемкость

Изменение энтропии ds.

Вычислим изохорную теплоемкость влажного водяного пара, имеющего степень сухости х 0 575 при давлении 1 бар. Поданным опытов А. М. Керимова, теплоемкости су и су при давлении р 1 бар равны соответственно 1 007 и 16 95 ккал / кг. Непосредственное вычисление по таблицам водяного пара дает значение cv 10 1 ккал / ( кг — град), практически не отличающееся от экспериментального.
 

Так как изохорная теплоемкость влажного пара cv — величина положительная, то это значит, что знаки дифференциалов dp и dv противоположны.
 

Так как изохорная теплоемкость влажного пара cv — величина положительная, то величины dp и dv — противоположны. Таким образом, изоэнтропическое расширение влажного пара обусловливает уменьшение его давления и температуры, а изоэнтропическое сжатие — возрастание их.
 

Так как изохорная теплоемкость влажного пара с есть положительная величина, то отсюда следует, что знаки дифференциалов dp и dv противоположны.
 

Результаты исследований изохорной теплоемкости на изохорах, проведенные вдали от критической точки v 2 67; 2 92; 4 95; 5 96; 9 92 см3 / г, показывают, что теплоемкость cv с увеличением температуры монотонно увеличивается, достигает некоторого своего максимального значения при определенной температуре, затем происходит скачкообразное ее уменьшение, что является признаком совершения перехода из двухфазного состояния в однофазное через пограничную кривую. В однофазной области в исследованном температурном интервале теплоемкость с на изохорах раствора данной концентрации с увеличением температуры монотонно уменьшается. Установлено, что величины теплоемкости сс в двухфазной области и их разрыв при переходе в однофазное состояние с ростом значения v возрастают.
 

Экспериментальное исследование изохорной теплоемкости некоторых углеводородов и спиртов.
 

Характер сингулярности изохорной теплоемкости одноком понентной жидкости таков, что до сих пор можно встретит утверждения, основанные на рассмотрении искаженного участ ка аномалии, об отсутствии расходимости этой величины в кри тической точке.
 

Уравнение для изохорной теплоемкости са записывается следующим образом ( г V сопз.
 

Следовательно, изохорную теплоемкость можно определить как количество теплоты, которое необходимо подвести к системе при постоянном объеме, чтобы повысить ее температуру на один градус.
 

Здесь Су — изохорная теплоемкость в идеальном состоянии, отнесенная к одной частице газа; Л, Л / — число положительных ионов и электронов.
 

Покажите, что изохорная теплоемкость этого газа не зависит от объема.
 

С г — изохорная теплоемкость газа; i CPICV; Pt и Р2 — начальное и конечное давление; СР — изобарная теплоемкость газа; TI и TZ — начальная и конечная температура; Vi и У2 — — начальный и конечный объем.
 

Зависимость изохорной теплоемкости от температуры для простых кристаллических веществ.| Изобарная теплоемкость металлов.

Таким образом, изохорная теплоемкость кристалла простого вещества должна быть равна 25 Дж / ( К-моль), Это правило соблюдается только при достаточно высоких температурах для многих металлов, начиная с четвертого периода системы элементов. Чем больше атомная масса элемента, тем при более низкой температуре достигается теоретическое значение теплоемкости. Теплоемкость алмаза не достигает этого значения даже при 1200 С.