Идеальный газ

Идеальные квантовые газы

В вышеупомянутом уравнении Сакура – ​​Тетроде лучший выбор константы энтропии оказался пропорциональным квантовой тепловой длине волны частицы, а точка, в которой аргумент логарифма обращается в ноль, примерно равна точке при при котором среднее расстояние между частицами становится равным тепловой длине волны. Фактически, сама квантовая теория предсказывает то же самое. Любой газ ведет себя как идеальный газ при достаточно высокой температуре и достаточно низкой плотности, но в точке, где уравнение Сакура – ​​Тетрода начинает разрушаться, газ начинает вести себя как квантовый газ, состоящий либо из бозонов, либо из фермионов . (См. Статью о газе в рамке для получения информации об идеальных квантовых газах, включая идеальный газ Больцмана.)

Когда температура достигает температуры Бойля, газы имеют тенденцию вести себя как идеальный газ в более широком диапазоне давлений .

Идеальный газ Больцмана

Идеальный газ Больцмана дает те же результаты, что и классический термодинамический газ, но делает следующую идентификацию для неопределенной постоянной Φ :

Φзнак равноТ32Λ3г{\ displaystyle \ Phi = {\ frac {T ^ {\ frac {3} {2}} \ Lambda ^ {3}} {g}}}

где Λ — тепловая длина волны де Бройля газа, а g — вырождение состояний.

Идеальные бозе- и ферми-газы

Идеальный газ бозонов (например, фотонный газ ) будет регулироваться статистикой Бозе – Эйнштейна, а распределение энергии будет иметь форму распределения Бозе – Эйнштейна . Идеальный газ фермионов будет определяться статистикой Ферми – Дирака, а распределение энергии будет иметь форму распределения Ферми – Дирака .

Определение 1-го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

∆U=Q-A.

Определение 1

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде: 

Q=∆U+A.

Определение 2

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая ΔU своей внутренней энергии.

Теплоемкость газов

При
проведении тепловых расчетов газопроводов
необходимо знать зна­чение удельных
теплоемкостей газов. Удельной теплоемкостью
газа называется количество тепла,
которое необходимо сообщить единице
массы (или объема) газа, чтобы температура
его в данном процессе изменилась на 1°
С.

Теплоемкость
газа зависит от характера протекаемого
процесса. Например, если в газгольдере
находится газ, который подогревается
на 1°С, но при этом в различных случаях
объем газа меняется по-разному. Работа
газа будет различной. В связи с этим и
теплоемкость газа будет не одинакова.
Она будет зависеть от характера
протекающего процесса.

Наибольшее
распространение в термодинамических
расчетах получили теплоемкости двух
простейших процессов: при постоянном
давлении С_ри
при постоянном объеме С_v.

В
каком-либо определенном процессе
изменения состояния газа количество
тепла, необходимое для нагревания 1 кг
газа на 1°С при данном давлении, зависит
от абсолютной температуры газа. Количество
тепла оказывается разным при различных
температурах газа. При данной температуре
газа количество тепла, необходимое для
нагревания 1 кг газа на 1°С, зависит от
величины давления.

Для городских
газопроводов теплоемкость газов
изменяется в узких пределах, поэтому
величину теплоемкости можно принимать
постоянной.

Значения
массовой теплоемкости С_рнекоторых
газов (в кДж/(кг∙К):

При
При

0°С
100°С

Бутан……….1,592 2,021

Воздух………1,003 1.010

Метан……….2,165 2.448

Пропан………1,549 2,016

В табл. 7.2 приведены
значения массовой теплоемкости при
постоянном давлении для метана в
зависимости от давления и температуры.
Для идеальных газов справедливо
соотношение (закон Майера):

(7.10)

гдес_р—
удельная теплоемкость при постоянном
давлении в Дж/(кг∙К); с_υ
— удельная теплоемкость при постоянном
объеме в Дж/(кг∙К); R—
газовая постоянная в Дж/(кг∙К).

Таким
образом, если известна величина удельной
теплоемкости при постоянном давлении,
можно определить теплоемкость при
постоянном объеме.

Массовые удельные
теплоемкости при постоянном давлении
и постоянном объеме идеальных газов
являются функцией только одной
температуры, т. е. зависят только от
температуры.

Таблица 7.2

Массовые
теплоемкости С_р(в
кДж/(кг∙К)
метана при постоянном давлении

Температура, °С	Давление, МПа
0,0980	1,010	2,020	3,030	4,040
-30 -20 -10 0,0 +10 +20 +30	2,022 2,064 2,110 2,152 2,192 2,231 2,273	2.106 2,148 2,185 2,223 2,261 2,298 2,336	2,223 2,244 2,269 2,307 2,340 2,378 2,407	2,370 2,360 2,370 2,395 2.424 2,457 2,483	2,554 2,499 2,487 2,491 2,512 2,537 2,554

Изопроцессы

С помощью уравнения объединённого газового закона можно исследовать процессы, в которых масса газа и один из важнейших параметров — давление, температура или объём — остаются постоянными. В физике такие процессы называются изопроцессами.

Из объединённого газового закона вытекают другие важнейшие газовые законы: закон Бойля-Мариотта, закон Гей-Люссака, закон Шарля, или второй закон Гей-Люссака.

Изотермический процесс

Процесс, в котором изменяются давление или объём, но температура остаётся постоянной, называется изотермическим процессом.

При изотермическом процессе T = const, m = const.

Поведение газа в изотермическом процессе описывает закон Бойля-Мариотта. Этот закон открыли экспериментальным путём английский физик Роберт Бойль в 1662 г. и французский физик Эдм Мариотт в 1679 г. Причём сделали они это независимо друг от друга. Закон Бойля-Мариотта формулируется следующим образом: В идеальном газе при постоянной температуре произведение давления газа на его объём также постоянно.

Уравнение Бойля-Мариотта можно вывести из объединённого газового закона. Подставив в формулу Т = const,получаем

p·V = const

Это и есть закон Бойля-Мариотта. Из формулы видно, что давление газа при постоянной температуре обратно пропорционально его объёму. Чем выше давление, тем меньше объём, и наоборот.

Как объяснить это явление? Почему же при увеличении объёма газа его давление становится меньше?

Так как температура газа не меняется, то не меняется и частота ударов молекул о стенки сосуда. Если увеличивается объём, то концентрация молекул становится меньше. Следовательно, на единицу площади придётся меньшее количество молекул, которые соударяются со стенками в единицу времени. Давление падает. При уменьшении объёма число соударений, наоборот, возрастает. Соответственно растёт и давление.

Графически изотермический процесс отображают на плоскости кривой, которую называют изотермой. Она имеет форму гиперболы.

Каждому значению температуры соответствует своя изотерма. Чем выше температура, тем выше расположена соответсвующая ей изотерма.

Изобарный процесс

Процессы изменения температуры и объёма газа при постоянном давлении, называются изобарными. Для этого процесса m = const, P = const.

Зависимость объёма газа от его температуры при неизменяющемся давлении также была установлена экспериментальным путём французским химиком и физиком Жозефом Луи Гей-Люссаком, опубликовавшем его в 1802 г. Поэтому её называют законом Гей-Люссака «При постоянном давлении отношение объёма постоянной массы газа к его абсолютной температуре является постоянной величиной».

При Р = const уравнение объединённого газового закона превращается в уравнение Гей-Люссака.

Пример изобарного процесса — газ, находящийся внутри цилиндра, в котором перемещается поршень. При повышении температуры растёт частота ударов молекул о стенки. Увеличивается давление, и поршень приподнимается. В итоге увеличивается объём, занимаемый газом в цилиндре.

Графически изобарный процесс отображается прямой линией, которая называется изобарой.

Чем больше давление в газе, тем ниже расположена на графике соответствующая изобара.

Изохорный процесс

Изохорным, или изохорическим, называют процесс изменения давления и температуры идеального газа при постоянном объёме.

Для изохорного процесса m = const, V = const.

Представить такой процесс очень просто. Он происходит в сосуде фиксированного объёма. Например, в цилиндре, поршень в котором не двигается, а жёстко закреплён.

Изохорный процесс описывается законом Шарля: «Для данной массы газа при постоянном объёме его давление пропорционально температуре». Французский изобретатель и учёный Жак Александр Сезар Шарль установил эту зависимость с помощью экспериментов в 1787 г. В 1802 г. её уточнил Гей-Люссак. Поэтому этот закон иногда называют вторым законом Гей-Люссака.

При V = constиз уравнения объединённого газового закона получаем уравнение закона Шарля, или второго закона Гей-Люссака.

При постоянном объёме давление газа увеличивается, если увеличивается его температура.

На графиках изохорный процесс отображается линией, которая называется изохорой.

Чем больше объём занимаемый газом, тем ниже расположена изохора, соответствующая этому объёму.

В реальности ни один параметр газа невозможно поддерживать неизменным. Это возможно сделать лишь в лабораторных условиях.

Конечно, в природе идеального газа не существует. Но в реальных разреженных газах при очень низкой температуре и давлении не выше 200 атмосфер расстояние между молекулами намного превышает их размеры. Поэтому их свойства приближаются к свойствам идеального газа.

• < Назад
• Вперёд >

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

1. Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

   Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.
3. Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ p = nkT или p — давление газа n — концентрация T — температура газа m — масса одной молекулы v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия Ек = mv2/2 Ек — кинетическая энергия m — масса тела v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы Ек = mv2/2 Ек — средняя кинетическая энергия поступательного движения молекулы m — масса молекулы v — скорость молекулы [м/с]

Из этой формулы можно выразить mv2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ p — давление газа n — концентрация E — средняя кинетическая энергия поступательного движения молекулы

Уравнение обращения воздействий

Исходными
уравнениями для вывода уравнения
обращения воздействий являются уравнение
неразрывности, уравнение состояния и
уравнение Бернулли для элементарной
струйки. Логарифмируя и дифференцируя
уравнение неразрывности G
= ρwF,
получаем:

=
+
(4.1)

Дифференцируя
уравнение состояния p
= ρRT,
после деления на ρполучаем:

=
R(dT + T)
(4.2)

Уравнение
Бернулли в дифференциальной форме имеет
вид:

=
— wdw
– dL_тех
— dL_тр
(4.3)

Из
(4.1) и (4.2) получаем:

=RdT
+ RT()(4.4)

Сопоставление
(4.4) с (4.3) после введения выражения для
скорости звука a2
= kRT
даёт следующее уравнение:

RdT
+
()
+ (w2
—
)+dL_тех
+ dL_тр
= 0
(4.5)

посколькуwdw
—
=(w2
—
)

От
члена RdTизбавимся
с помощью дифференциального уравнения
энергии:

dQ_н
= di + d=RT
+ wdw +(4.6)

(так
как di
=c_pdT
=dT)

Подставляем
(4.6) в (4.5) и после несложных преобразований
получаем уравнение
обращения воздействий,
связывающее изменение скорости потока
с внешними воздействиями – геометрическим,
расходным, механическим, тепловым и
воздействием трения:

(M2
— 1)
=-(4.7)

где
в правой части уравнения указанные выше
воздействия по порядку.

Уравнение
обращения воздействий было выведено
Л.А.Вулисом и может рассматриваться как
условие обращения воздействий, поскольку
устанавливает условия, при которых
возможен переход через скорость звука,
то есть через критическое значение
скорости. Из уравнения обращения
воздействий следует очень важный вывод:односторонним
воздействием нельзя перевести скорость
дозвукового потока через критическое
значение, то есть в сверхзвуковую область
– для этого нужно сменить знак воздействия.

Наиболее
часто в технике мы встречаемся с
геометрическим воздействием, которое
имеет место в сопле Лаваля, представляющее
собой внач але сужающийся, а затем, после
критического сечения, расширяющийся
канал. Если прочие воздействия отсутствуют,
то уравнение для геометрического
воздействия принимает вид:

=(4.8)

Уравнение
(4.8) носит также название уравнение
Гюгонио,
которое
было выведенонезависимо
от уравнения (4.7) из уравнений неразрывности
и Бернулли. Анализируя это уравнение,
видим, что для ускорения дозвукового
потока сопло должносужающимся,
так как при MdF

Для
получения сверхзвукового потока после
достижения скорости звукав
критическом сечении сопло должно быть
расширяющимся, тка как при MdF

Скорость
потока и безразмерная площадь проходного
сечения сопла Лаваля
связаныоднозначным
соотношением, которое графически
представлено на рис. 4.1.

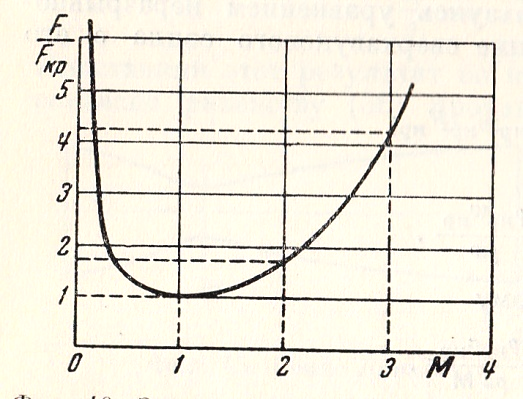
Рис.4.1.
Зависимость безразмерной площади сопла
Лаваля от числа M

Давление,
температура и плотность газа в идеальном
термодинамическом процессе связаныуравнением
состояния
и, таким образом, в произвольном сечении
сопла Лаваля имеется определённое
значения числа Маха, которое зависит
от полного давления в камере перед
соплом. Соответственно, так как статическое
давление в сечениях сопла определяется
числом Маха, то давление на срезе
сверхзвукового сопла зависит только
от давления в камере перед соплом и от
формы сопла. Расчёт течений в соплах и
диффузорах представлен ниже в этой
главе.

В
каждом воздействий из другихвоздействий
для перехода через критическую скорость
(M
= 1)
нужно изменить знак воздействия.
Например, в расходном сопле для ускорения
потока на дозвуковом участке нужно
подводить дополнительную массу жидкости,
а на сверхзвуковом участке отводить
её. В тепловом сопле подводом тепла к
движущемуся газу можно увеличить его
скорость только до критического значения,
а для перехода через скорость звука
нужно отводить тепло. Аналогично обстоит
дело с механическим соплом. В дозвуковой
области нужно подводить работу
(компрессор), а в сверхзвуковой – отводить
(турбина). Только трение является
односторонним воздействием, поскольку
оно всегда существует и его нельзя
отвести. Работа сил трения всегда
положительна, и переход через скорость
звука воздействие трения невозможен.

Изотермический процесс (T=const)

Определение 10

При протекании квазипроцесса с постоянным параметром Т говорят об изотермическом процессе.

Из уравнения pV=νRT=mMRT имеем, что неизменные температура Т с количеством вещества ν – это постоянное состояние для произведения значения давления газа p на его объем V:

pV=const.

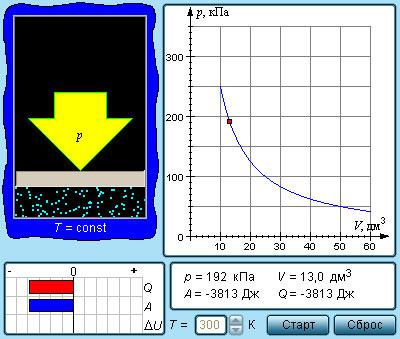
Рисунок 3.3.1. Модель изотермического процесса.

Определение 11

Изображение изотермических процессов на плоскости (p, V) предусматривает различные значения температур Т гипербол p~1V. Они получили название изотермов.

Коэффициент пропорциональности данного отношения увеличивается с ростом Т. Рисунок 3.3.2 показывает, что при меньшей Т подразумевает уменьшение V. В 1662 году было получено уравнение изотермического процесса Р. Бойлем, а позднее Э. Мариоттом в 1676 году. Отсюда и сложное его название – закон Бойля-Мариотта.

Рисунок 3.3.2. Семейство изотерм на плоскости (p, V). T3>T2>T1.

1Вопрос Основные термодинамические параметры состояния газа.

Давление 
Р
– мера силы, которая действует на единицу
поверхности: 
Р
= lim ∆Fn / ∆S = dFn/ dS, 
где
DS → 0; ∆Fn – сила, направленная
перпендикулярно участку поверхности. 

Удельный
объем 
V
– величина, обратная плотности
rвещества: 
v
= 1 / r= dV/ dm, 
где
dV– бесконечно малый элемент объема; 
dm–
масса вещества. 

Моль 
Количество
вещества, которое содержит число молекул,
равное числу атомов, содержащихся в 12
г изотопа углерода 12С, называется
молем. 

Число
Авогадро 
NA=
6,02 ч 1023 моль-1. Величина, необходимая при
расчетах. Показывает, сколько молекул
содержится в одном моле любого
вещества. 

Молярная
масса 
М
– масса одного моля: 
М
= NAm × 1а. е. м, 
где
NA– число Авогадро; 
m–
молекулярная масса. 
Молярная
масса = кг/моль и молярный объем =
м3/моль. 

Объем
одного моля – молярный объем: 
VM
= M / r 
где
M– молярная масса; 
r–
плотность вещества. 

Формулы
для определения числа молей вещества
и числа молекул вещества имеют следующий
вид: 
u=
m /M= V/ VM, 
N
= uNA= (m / M)NA = (V/ VM)NA. 

Температура 
За
меру температуры принято брать среднюю
кинетическую энергию поступательного
движения молекул. Если два тела при
соприкосновении не обмениваются энергией
путем теплообмена, можно говорить, что
эти тела имеют одинаковую температуру
и в системе существует тепловое
равновесие.

2вопрос:
Материальный баланс процесса горения:
Для расчета процессов
горения
твердого и жидкого
топлива составляют материальный баланс
процесса горения.

Материальный
баланс процесса горения выражает
количественные соотношения между
исходными веществами (топливо, воздух)
и конечными продуктами (дымовые газы,
зола, шлак) При сжигании твердого и
жидкого топлива горючие вещества могут
окисляться с образованием оксидов
различной степени окисления.
Стехиометрические уравнения
реакций горения углерода, водорода и
серы можно записать так:

а)
С+О₂=СО₂;

б)
С+(1/2)·О₂=СО;

в)
S+О₂=SО₂;

г)
H2+(1/2)·О₂=H₂О;

При расчете объемов воздуха и продуктов
сгорания условно принимают, что все
горючие вещества окисляются полностью
с образованием только оксидов с наивысшей
степенью окисления (реакции а, в, г).

Из уравнения (а)следует, что для полного окисления 1
кмоль углерода (12 кг) расходуется 1 кмоль,
т. е. 22,4 м3, кислорода и образуется 1 кмоль
(22,4 м3) оксида углерода. Соответственно
для 1 кг углерода потребуется 22,4/12 = 1,866
м3 кислорода и образуется 1,866 м3 СО2.
В 1 кг топлива содержится Сp/100 кг углерода.
Для его горения необходимо 1,866·Сp/100
м3 кислорода и при сгорании образуется
1,866 Сp/100 м3 CO2.

Аналогично из уравнений
(в) и (г)на окисление горючей серы
(μs = 32), содержащейся в 1 кг топлива,
потребуется (22,4/32) Spл/100 м3 кислорода
и образуется такой же объем SO2. А на
окисление водорода (),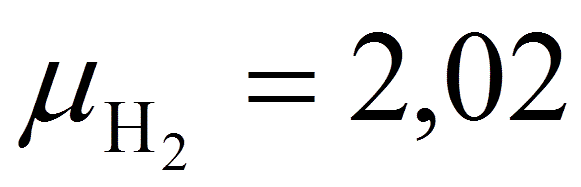
содержащегося в 1 кг топлива, потребуется
0,5·(22,4/2,02) Нp/100 м3 кислорода и образуется
(22,4/2,02) Нp/100 м3 водяного пара.

Суммируя полученные выражения и учитывая
кислород, находящийся в топливе(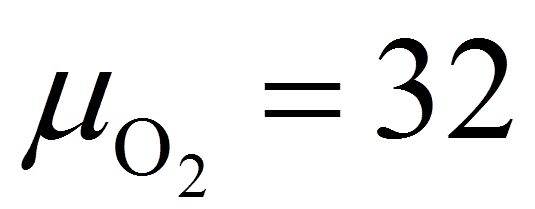),после
несложных преобразований получим
формулу для определения количества
кислорода, теоретически необходимого
для полного сжигания 1 кг твердого или
жидкого топлива, м3/кг:

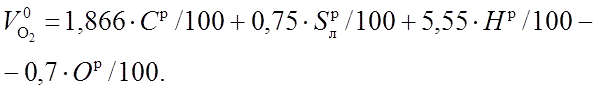
В воздухе содержится кислорода примерно
21 % по объему, поэтому количество воздуха,
теоретически необходимое для полного
сжигания 1 кг топлива V0, м3/кг, составляет:

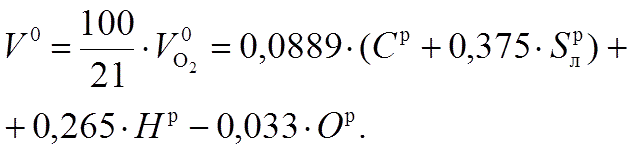
В процессе полного горения с теоретически
необходимым количеством воздуха
образуются газообразные продукты,
которые состоят из CO2, SO2, N2 и H2O — оксиды
углерода и серы являются сухими
трехатомными газами. Их принято объединять
и обозначать через RO2 = CO2 + SO2.

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

Классический термодинамический идеальный газ

Классические термодинамические свойства идеального газа можно описать двумя уравнениями состояния :

Закон идеального газа

Связь между законами Бойля , Шарля , Гей-Люссака , Авогадро , комбинированного и идеального газа с постоянной Больцмана k _B =рN _A знак равно п RN (в каждом законе свойства, обведенные кружком, являются переменными, а свойства, не обведенные кружком, считаются постоянными)

Закон идеального газа — это уравнение состояния идеального газа, которое определяется следующим образом:

куда

• P — давление
• V — объем
• n — количество вещества в газе (в молях )
• R — газовая постоянная (0,08206  л · атм · K −1 · моль −1 )
• Т — абсолютная температура .

Закон идеального газа — это расширение экспериментально обнаруженных законов газа . Это также может быть получено из микроскопических соображений.

Реальные жидкости при низкой плотности и высокой температуре приблизительно соответствуют поведению классического идеального газа. Однако при более низких температурах или более высокой плотности реальная жидкость сильно отличается от поведения идеального газа, особенно когда она конденсируется из газа в жидкость или осаждается из газа в твердое тело. Это отклонение выражается коэффициентом сжимаемости .

Это уравнение получено из

• Закон Бойля : ;V∝1п{\ displaystyle V \ propto {\ frac {1} {P}}}
• Закон Чарльза : ;V∝Т{\ Displaystyle V \ propto T}
• Закон Авогадро : .V∝п{\ Displaystyle V \ propto n}

Объединив три закона, получим

V∝пТп{\ displaystyle V \ propto {\ frac {nT} {P}}}

Это:

Vзнак равнор(пТп){\ displaystyle V = R \ left ({\ frac {nT} {P}} \ right)}

пVзнак равнопрТ{\ displaystyle PV = nRT}.

Внутренняя энергия

Другое уравнение состояния идеального газа должно выражать , согласно которому внутренняя энергия фиксированной массы идеального газа является функцией только его температуры. Для наших целей удобно постулировать примерную версию этого закона, написав:

Uзнак равноc^VпрТ{\ displaystyle U = {\ hat {c}} _ {V} nRT}

куда

• U — внутренняя энергия
• ĉ _V — безразмерная удельная теплоемкость при постоянном объеме, приблизительно32для одноатомного газа ,52для двухатомного газа и 3 для нелинейных молекул, если рассматривать трансляции и вращения классически и игнорировать квантовый колебательный вклад и электронное возбуждение. Эти формулы возникают в результате применения классической теоремы о равнораспределении к поступательным и вращательным степеням свободы.

То, что U для идеального газа зависит только от температуры, является следствием закона идеального газа, хотя в общем случае ĉ _V зависит от температуры, и для вычисления U необходим интеграл .

Микроскопическая модель

Чтобы перейти от макроскопических величин (левая часть следующего уравнения) к микроскопическим (правая часть), мы используем

прзнак равноNkB{\ displaystyle nR = Nk _ {\ mathrm {B}}}

куда

• N{\ displaystyle N} количество частиц газа
• kB{\ Displaystyle к _ {\ mathrm {B}}}- постоянная Больцмана (1,381 × 10 −23  Дж · К −1 ).

Распределение вероятностей частиц по скорости или энергии дается распределением скорости Максвелла .

Модель идеального газа зависит от следующих предположений:

• Молекулы газа неразличимы, маленькие, твердые сферы.
• Все столкновения упругие, и любое движение происходит без трения (без потерь энергии при движении или столкновении)
• Применяются законы Ньютона
• Среднее расстояние между молекулами намного больше, чем размер молекул.
• Молекулы постоянно движутся в случайных направлениях с распределением скоростей
• Между молекулами нет сил притяжения или отталкивания, кроме тех, которые определяют их точечные столкновения.
• Единственные силы между молекулами газа и окружающей средой — это те, которые определяют точечные столкновения молекул со стенками.
• В простейшем случае нет дальнодействующих сил между молекулами газа и окружающей средой.

Предположение о сферических частицах необходимо для того, чтобы не было разрешенных вращательных мод, в отличие от двухатомного газа. Следующие три предположения очень взаимосвязаны: молекулы твердые, столкновения упругие, межмолекулярные силы отсутствуют. Предположение о том, что пространство между частицами намного больше, чем сами частицы, имеет первостепенное значение и объясняет, почему приближение идеального газа не работает при высоких давлениях.

Термодинамические потенциалы

Выражая энтропию как функцию T , V и N :

SkNзнак равнопер⁡(VТc^VNΦ){\ displaystyle {\ frac {S} {kN}} = \ ln \ left ({\ frac {VT ^ {{\ hat {c}} _ {V}}} {N \ Phi}} \ right)}

Химический потенциал идеального газа рассчитывается из соответствующего уравнения состояния (см термодинамического потенциала ):

μзнак равно(∂г∂N)Т,п{\ displaystyle \ mu = \ left ({\ frac {\ partial G} {\ partial N}} \ right) _ {T, P}}

где G — свободная энергия Гиббса и равна U + PV — TS, так что:

μ(Т,п)знак равноkТ(c^п-пер⁡(kТc^ппΦ)){\ displaystyle \ mu (T, P) = kT \ left ({\ hat {c}} _ {P} — \ ln \ left ({\ frac {kT ^ {{\ hat {c}} _ {P}) }} {P \ Phi}} \ right) \ right)}

Химический потенциал обычно соотносится с потенциалом при некотором стандартном давлении P o, так что при :
μо(Т)знак равноμ(Т,по){\ displaystyle \ mu ^ {o} (T) = \ mu (T, P ^ {o})}

μ(Т,п)знак равноμо(Т)+kТпер⁡(ппо){\ displaystyle \ mu (T, P) = \ mu ^ {o} (T) + kT \ ln \ left ({\ frac {P} {Po}} \ right)}

Для смеси ( j = 1,2, …) идеальных газов, каждый из которых имеет парциальное давление P _j , можно показать, что химический потенциал μ _j будет задан приведенным выше выражением с заменой давления P на P _j .

Термодинамические потенциалы идеального газа теперь могут быть записаны как функции от T , V и N как:

U{\ Displaystyle U \,}		знак равноc^VNkТ{\ displaystyle = {\ hat {c}} _ {V} NkT \,}
А{\ Displaystyle A \,}	знак равноU-ТS{\ Displaystyle = U-TS \,}	знак равноμN-NkТ{\ Displaystyle = \ му N-NkT \,}
ЧАС{\ Displaystyle H \,}	знак равноU+пV{\ Displaystyle = U + PV \,}	знак равноc^пNkТ{\ displaystyle = {\ hat {c}} _ {P} NkT \,}
г{\ Displaystyle G \,}	знак равноU+пV-ТS{\ Displaystyle = U + PV-TS \,}	знак равноμN{\ displaystyle = \ mu N \,}

где, как и раньше,

c^пзнак равноc^V+1{\ displaystyle {\ hat {c}} _ {P} = {\ hat {c}} _ {V} +1}.

Наиболее информативный способ записать потенциалы в терминах их естественных переменных, поскольку каждое из этих уравнений может использоваться для вывода всех других термодинамических переменных системы. В терминах их естественных переменных термодинамические потенциалы однокомпонентного идеального газа равны:

U(S,V,N)знак равноc^VNk(NΦVеSNk)1c^V{\ Displaystyle U (S, V, N) = {\ hat {c}} _ {V} Nk \ left ({\ frac {N \ Phi} {V}} \, e ^ {S / Nk} \ right ) ^ {1 / {\ hat {c}} _ {V}}}

А(Т,V,N)знак равноNkТ(c^V-пер⁡(VТc^VNΦ)){\ Displaystyle A (T, V, N) = NkT \ left ({\ hat {c}} _ {V} — \ ln \ left ({\ frac {VT ^ {{\ hat {c}} _ {V) }}} {N \ Phi}} \ right) \ right)}

ЧАС(S,п,N)знак равноc^пNk(пΦkеSNk)1c^п{\ Displaystyle H (S, P, N) = {\ hat {c}} _ {P} Nk \ left ({\ frac {P \ Phi} {k}} \, e ^ {S / Nk} \ right ) ^ {1 / {\ hat {c}} _ {P}}}

г(Т,п,N)знак равноNkТ(c^п-пер⁡(kТc^ппΦ)){\ Displaystyle G (T, P, N) = NkT \ left ({\ hat {c}} _ {P} — \ ln \ left ({\ frac {kT ^ {{\ hat {c}} _ {P) }}} {P \ Phi}} \ right) \ right)}