Как найти среднюю скорость

Оптимальная скорость для автомобиля — второй фактор выбора режима поездки

Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим. Тем не менее, существуют определенные рекомендации от производителей.

Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:

• на обгоне автомобиль вынужден потреблять в разы больше топлива в силу необходимости быстрого разгона;
• постоянное торможение и трогание с места в пробке или на различных преградах также дает плюс к расходу;
• движение на скорости свыше 100 километров в час начинает значительно увеличивать расход бензина;
• производитель рассчитывает трассовые режимы поездки на среднюю скорость 90 километров в час;
• под данный показатель происходит настройка всех функций и узлов автомобиля, передаточных числе и двигателя.

Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.

Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости:

Примеры решения задач

Задание. Движение материальной точки А задано уравнением: $x=2 t^-4 t^$ . Точка начала свое движение при t=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Формула скорости не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$ begin10 t-t^=10(2.2) t_=5+sqrt approx 8,8(c) ; t_=5-sqrt approx 1,13(c) end $$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

При решении уравнения (2.3) нам подойдет корень равный:

Ответ. 1) $x=0 mathrm

m>$ 2) $t_=8,8 mathrm, t_=1,13 c, t_=11 c$

Класс: 4

Цели:

• закрепить знания нахождения скорости, времени, расстояния;
• ввести формулы;
• учиться решать задачи с этими величинами по формулам и без них;
• развивать мышление и память;
• прививать любовь к математике.

1. Организация учащихся.

2. Сообщение темы.

— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.

— А работать мы будем в форме соревнований трех команд:

• 1 ряд — автомобилисты
• 2 ряд — летчики
• 3 ряд — мотоциклисты

— Баллы будем выставлять на доске

3. Соотнести записи с картинкой.

— Как вы думаете, что написано на доске? (Скорости)

— Соотнесите их с нужной картинкой.

(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.

Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.

— Как вы понимаете км/сек, км/ч, м/мин.

а) В тетрадь записываете ответ с наименованием.

Таблица на интерактивной доске.

Угловая скорость

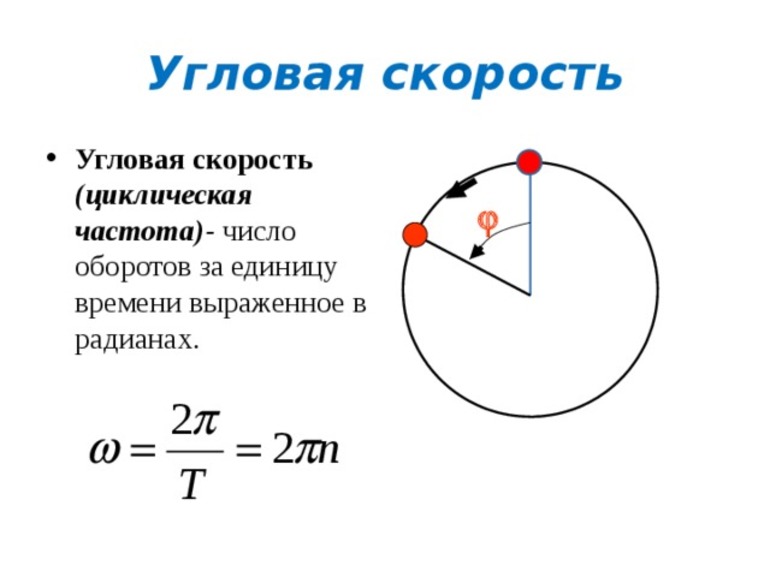
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = , где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Скорость в свободных условиях движения

В свободных условиях, когда дорога относительно пустая и вы можете выбирать скорость по своему усмотрению, казалось бы, все просто. Если следовать ПДД, то это 60 км/ч в городе, 80 км/ч на некоторых городских магистралях, 100 км/ч на МКАД, 90 км/ч за городом и 110 км/ч на магистрали. Ну и для любителей поиграть в кошки-мышки с законом, можно на эти значения набросить те самые «беспошлинные» 20 км/ч – ниже этого превышения штрафов нет. Но я сейчас не о штрафах, а о безопасности. Представим, что ограничений скорости нет, как, скажем на автобанах Германии. Значит, можно безнаказанно ехать с любой скоростью. А с какой скоростью ехать безопасно?

Безопасность = наличие резерва

Вспомним, что одно из условий совершения маневра – наличие запаса тяги. И что тяга двигателя – крутящий момент – зависит от показаний тахометра (см. статью «Безопасность вождения и крутящий момент двигателя»). Но способность двигателя разгонять машину зависит также и от скорости: чем ближе скорость движения автомобиля к максимальной, тем сложнее ускориться. Автомобиль хорошо ускоряется при небольших скоростях, и по мере приближения к максимальной скорости разгон происходит все медленнее. Кстати, еще несколько лет назад в технических характеристиках автомобилей BMW на сайте производителя приводилось два показателя времени разгона: для разгона от 0 до 100 км/ч и от 80 до 120 км/ч. Эти показатели были примерно равны между собой. То есть при разгоне с места автомобилю нужно столько же времени для ускорения на 100 км/ч, сколько при разгоне на большой скорости для ускорения всего на 40 км/ч. Чувствуете, к чему я клоню?

Даже если бы и была возможность хоть каждый день ездить на «максималке», все равно этого делать не стоит, потому что любое устройство, в том числе и двигатель, работая на максимуме, не имеет резерва.

Крейсерская скорость

Для сохранения запаса тяги двигателя необходимо ограничивать скорость движения и не приближаться к максимальному значению скорости. А насколько можно приближаться? Где граница? Оптимальная скорость составляет 60-70% от максимальной и называется крейсерской скоростью. Крейсерская скорость движения автомобиля – и есть та разумная граница, которую не стоит превышать, даже на свободных магистралях. То есть крейсерская скорость – максимальная безопасная скорость движения АВТОМОБИЛЯ.

Крейсерская скорость также является самой выгодной скоростью движения в плане соотношения времени в пути к расходу топлива, поэтому воздушные суда летают с крейсерской скоростью.

Перейду к конкретике. Например, для ВАЗ-2110 максимальная скорость по паспорту – 180 км/ч, а крейсерская скорость составляет 108 км/ч (60%). А если взять VW Touareg мощностью 240 л.с., то у него «максималка» по паспорту – 218 км/ч. И для него крейсерская скорость составит 130 км/ч. Не сильно больше, чем у «Лады», правда?

Таким образом, чтобы всегда иметь запас тяги мотора на случай экстренных действий и быть в безопасности, не превышайте крейсерскую скорость своей машины даже в свободных условиях движения. А поскольку максимальная разрешенная скорость в России – 130 км/ч, то нет и проблемы превышения крейсерской скорости Так что соблюдайте правила, и все у вас будет в порядке!

Средняя скорость

Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.

Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла

Рис. 6. Иллюстрация к примеру

Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.

Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).

Рис. 7. Средняя скорость

Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.

Рис. 8. Перемещение равно 0

На практике чаще всего используется понятие средней путевой скорости.

Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).

Рис. 9. Средняя путевая скорость

Существует еще одно определение средней скорости.

Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.

Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:

Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.

Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).

Рис. 10. Иллюстрация к задаче

Дано:Найти:

Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем

Средняя скорость равна:

Полный путь (

Путь подъема на склон равен:

Путь спуска со склона равен:

Время, за которое пройден полный путь, равно:

Ответ:

Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.

Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость

Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).

Рис. 11. Спидометр автомобиля показывает мгновенную скорость

Существует еще одно определение мгновенной скорости.

Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).

Рис. 12. Мгновенная скорость

Для того чтобы лучше понять данное определение, рассмотрим пример.

Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.

Рис. 13. График зависимости проекции перемещения от времени

На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 14. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 15. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть

A

Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.

Направление мгновенной скорости совпадает с направлением перемещения тела.

Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).

Рис. 16. Направление мгновенной скорости

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Постоянная скорость

Описание формулы.

Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.

А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).

Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).

График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.

Это интересно: Как найти по номеру машины владельца — пробиваем авто по базам

Характеристика величины

Скорость в физике — это величина, описывающая количество пути, пройденного за единицу времени. То есть когда говорят, что скорость пешехода составляет 5 км/ч, это означает, что он проходит расстояние в 5 км за 1 час.

Единой размерности в этой формуле нет, поскольку с ее помощью описываются и крайне медленные, и очень быстрые процессы.

Например, искусственный спутник Земли преодолевает порядка 8 км за 1 секунду, а тектонические плиты, на которых расположены материки, по измерениям ученых, расходятся всего на несколько миллиметров за год. Поэтому и размерности у скорости могут быть разными — км/ч, м/с, мм/с и т.д.

Принцип заключается в том, что расстояние делится на время, необходимое для преодоления пути. Не стоит забывать о размерности, если проводятся сложные расчеты.

Чтобы не запутаться и не ошибиться в ответе, все величины приводятся в одни и те же единицы измерения. Если длина пути указана в километрах, а какая-то его часть в сантиметрах, то, пока мы не получим единства в размерности, правильного ответа нам не узнать.

Мгновенная и средняя скорость

Скорость движения материальной точки — это физическая величина, характеризующая быстроту движения и равная отношению пройденной длины ко времени, за которое эта длина была пройдена:

$$v={Δl \over Δt}$$

Поскольку длина в системе СИ измеряется в метрах, а время — в секундах, то скорость измеряется в метрах в секунду.

Рис. 1. Скорость движения в физике

Наиболее точной является мгновенная скорость, то есть такая скорость, при которой величина $Δt$ стремится к нулю. При этом получающееся значение скорости $v$ может быть постоянным, а может меняться в каждой точке пройденного пути.

Вычисление мгновенной скорости позволяет моделировать движение материальной точки наиболее детально. Однако в реальных условиях настолько большая точность чаще всего не требуется

Как правило, важно, чтобы движение было совершено к определённому моменту времени, а как именно это произошло — не имеет значения

В этом случае используется понятие средней скорости. Средняя скорость отличается от мгновенной тем, что для вычисления используется сразу весь отрезок времени. Величина $Δt$ в приведённой формуле равна общему времени движения:

$$v_{ср}={l_{общ} \over t_{общ}}$$

Расстояние, длина пройденного пути

Здесь будет легче сориентироваться, скорее всего, автомобилистам, у которых есть счетчик пробега в машине. Они смогут определить, сколько километров проехали, а еще и скорость знают. Но так как движение неравномерное, то установить тоное время перемещения не получится, если только мы возьмем среднюю скорость.

Формула пути (расстояния) – произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности

Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см

Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».

Как рассчитать скорость бега

Скорость показывает, какое расстояние вы преодолеваете в единицу времени. Может измеряться в метрах в секунду или в километрах в час.

Скорость – первый критерий, главная мера для бегунов. Даже несмотря на то, что спортивные часы чаще фиксируют наш темп, чем скорость. При этом темп (pace) – величина, обратная скорости (speed). Темп измеряется в минутах на километр и показывает, сколько времени тратит человека на преодоление определенного расстояния.

Формула расчёта скорости:

Скорость (км/ч) = (расстояние/время в минутах)*60
Темп (мин/км) = время в минутах/расстояние

Формула расчёта скорости из показателя темпа:

Следите за новостями из мира бега в нашем телеграм-канале Бегущая строка.
Пишем коротко и по делу.

Скорость = 60/темп (км/ч) или 50/3*темп (м/с)

Анализ методов определения скорости автомобиля при ДТП

По тормозному следу

Достоинства:

• относительная простота метода;
• большое количество научных работ и составленных методических рекомендаций;
• достаточно точный результат;
• возможность быстрого получения результатов экспертизы.

Недостатки:

• при отсутствии следов шин (если автомобиль, к примеру, не тормозил перед столкновением, или особенности дорожного покрытия не позволяют с достаточной достоверностью измерить след юза) проведение данного метода невозможно;
• не учитывается воздействие одного транспортного средства в ходе столкновения на другое, что может.

По закону сохранения количества движения

Преимущества:

• возможность определения скорости транспортного средства даже при отсутствии следов торможения;
• при тщательном учёте всех факторов метод имеет высокую достоверность результата;
• удобство использования метода при перекрёстных столкновениях и столкновениях с неподвижными автомобилями.

Недостатки:

• отсутствие данных о режиме движения транспортного средства приводит к неточному результату;
• по сравнению с предыдущим методом более сложные и громоздкие вычисления;
• метод не учитывает энергию, затраченную на образование деформаций.

Исходя из полученных демормаций

Преимущества:

• учитывает затраты энергии на образование деформаций;
• не требует наличия следов торможения.

Недостатки:

• сомнительная точность получаемых результатов;
• огромное количество учитываемых факторов;
• зачастую невозможность определения многих факторов;
• отсутствие стандартизированных воспроизводимых методик определения.

На практике чаще всего используют два метода – определение скорости по следу торможения и исходя из закона сохранения количества движения. При использовании двух этих методов одновременно обеспечивается максимально точный результат, так как методики дополняют друг друга.

Остальные способы определения скорости транспортного средства значительного распространения не получили по причине недостоверности получаемых результатов и/или необходимости громоздких и сложных вычислений. Также при оценке скорости автомобиля учитывают показания свидетелей происшествия, хотя в таком случае нужно помнить о субъективности восприятия скорости разными людьми.

В некоторой мере помочь разобраться с обстоятельствами происшествия и в итоге получить более точный результат может помочь анализ видео из камер наблюдения и видеорегистраторов.

Источник