Без бумаг и инспекторов дтп можно будет оформить в мобильном приложении

Шаги

Метод 1 из 2:

Часть 1: Определение средней скорости изменения функции

1. 1

   Функция. Это соответствие между переменными величинами, в котором каждому значению некоторой независимой переменной «x» соответствует определенное значение зависимой переменной «у».

2. 2

   Переменная. Это величина, в процессе своего изменения принимающая различные значения. Переменные, как правило, обозначаются через «х» и «у».

3. 3

   Угловой коэффициент. Он равен тангенсу угла между положительным направлением оси абсцисс и данной прямой линией. Угловой коэффициент характеризует скорость изменения линейной функции.

4. 4

   Секущая. Это прямая, пересекающая две или более точки, лежащих на кривой. При вычислении средней скорости изменения функции вы находите угловой коэффициент секущей между двумя заданными точками.

5. 5

   Основная формула для вычисления средней скорости изменения функции показана на рисунке.

Метод 2 из 2:

Часть 2: Вычисление средней скорости изменения функции

1. 1

   Найдите f(x + h).

   Вычислите f(x + h), используя следующее выражение: f(x + h) = (х + h)^2 = x^2 + 2xh + h^2.

   В исходной функции f(x) замените «х» на «x + h», где h – приращение аргумента (то есть изменение независимой переменной «х»).Например, дана функция f(х) = x^2. Вычислите среднюю скорость изменения функции между в интервале (2,5) (то есть х1 = 2 и х2 = 5).

2. 2

   Вычислите среднюю скорость изменения, воспользовавшись основной формулой и подставив в нее исходную функцию f(x) и преобразованную функцию f(x+h).

   В приведенном выше примере вычисления показаны на рисунке.
   WH.shared.addScrollLoadItem(‘cc51182fbff452ca00cb398923769107’)

   {«smallUrl»:»https:\/\/www.wikihow.com\/images_en\/thumb\/e\/e7\/Screen-Shot-2014-03-11-at-5.00.07-PM.png\/460px-Screen-Shot-2014-03-11-at-5.00.07-PM.png»,»bigUrl»:»https:\/\/www.wikihow.com\/images\/thumb\/e\/e7\/Screen-Shot-2014-03-11-at-5.00.07-PM.png\/728px-Screen-Shot-2014-03-11-at-5.00.07-PM.png»,»smallWidth»:460,»smallHeight»:111,»bigWidth»:»728″,»bigHeight»:»176″,»licensing»:»

   «}

3. 3

   Найдите h.

   В приведенном выше примере: h = x2 — x1 = 5 — 2 = 3.

   Для этого вычтите начальное значение переменной «х» из ее конечного значения. Другими словами, если интервал задается в виде (x1, x2), то h = x2 — x1.

4. 4

   Вычислите среднюю скорость изменения.

   В приведенном выше примере: А(х) = 2х + h = 2 × 2 + 3 = 7

   Поставьте найденное значение h в выведенную выше формулу (вместо «х» подставьте значение x1).

5. 5

   Запишите ответ. В нашем примере средняя скорость изменения функции равна 7.

За что любят грузовики

На просторах нашей Родины нереально большое количество фур, самосвалов, газелей и прочих говновозов всех мастей и размеров. Они медленно тащатся по трассам и по городам, жутко воняя и издвая «приятный и не громкий» для нежных ушей граждан звук. Разумеется, быстрее 80 км/ч они не едут в принципе: либо тахограф не пускает, либо арбузы. Поворачивают они в шесть раз медленнее легковушки. Обгоняя своих собратьев, останавливают левый ряд на пару минут. Из-за этих уродов постоянные пробки на любых перекрестках, потому как повернуть сразу они не могут, а светофор горит достаточно недолго. Как результат — вместо 20 легковушек поворачивает 2 фуры, да и то если не заглохли на светофоре. А если учесть, что сама фура длиной как 5 джипов, то пробка растягивается на километры. И так везде. Своим присутствием на дорожном полотне они мстят и гадят другим водителям.

2 Проверка нагревания электрических машин

Проверку
на нагревание электрических машин
тепловоза следует выполнять, руководствуясь
построенной кривой токаи кривой времени.

Для
тепловозов 3ТЭ3 и ТЭ3 на нагревание
проверяются обмотка якоря генератора,
а для тепловозов 3ТЭ10М, 2ТЭ10М, 2ТЭ121,
2ТЭ116, 2М62, 2ТЭ121 проверяем обмотки якорей
тяговых электродвигателей. По заданию
у нас тепловоз 4ТЭ121, значит, будем
производить проверку на нагревание
обмотки якорей тяговых электродвигателей.

Для
расчетов по проверке обмоток электромашин
на нагревание используем следующую
формулу:

τ_∞·

где
превышение температуры обмоток генератора
или тягового электродвигателя над
температурой окружающей среды, С;

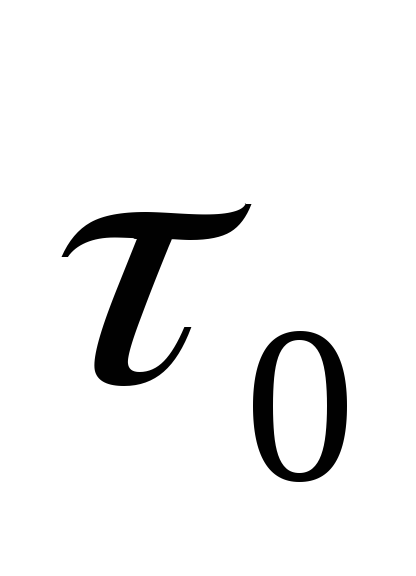начальное
превышение температуры обмоток для
расчетного промежутка времениС;

промежуток
времени, в течение которого величина
тока принимается постоянной, мин;

установившееся
превышение температуры обмоток
электромашины над температурой
окружающего воздуха С;

T

тепловая постоянная времени, мин;

Установившееся
превышение температуры обмотоки постоянная времениT
являются тепловыми параметрами
(характеристиками) тяговой электрической
машины.

Для
определения значенийиT
необходимо пользоваться графическими
зависимостямииT
от тока нагрузки для тяговых электрических
машин тепловоза.

Расчетные
интервалы временивыбираем так, чтобы было выдержано
соотношение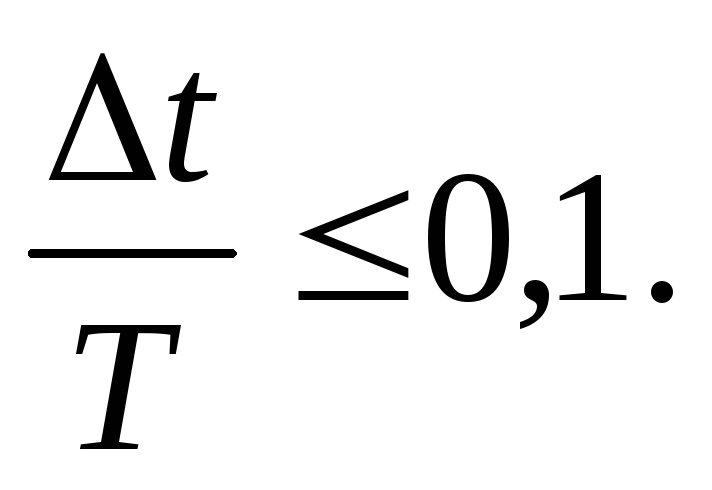

При
определении средней величины тока
электрических машин тепловоза для
отыскания тепловых параметров Т иследует кривую токаразбить на отдельные отрезки, в пределах
которых величину тока следует принимать
постоянной, равной полу сумме токов в
начале и конце отрезка.

Значение
тока тягового электродвигателя для
нашего тепловоза 4ТЭ121 определяется
делением тока генератора I_г
на шесть (т.к. в силовую цепь включено 6
тяговых электродвигателей).

Изменение
температуры электромашин при движении
тепловоза на режимах холостого хода и
торможения определяется по формуле:

Первоначальное
превышение температуры обмоток тяговых
электромашин в момент отправления
поезда со станции «А» следует принимать
равным=+15С.

Максимально
допустимое превышение температуры
обмоток якорей тяговых электрических
машин над температурой окружающего
воздуха составляет для нашего тепловоза

140С.

Все
расчеты по определению температур
обмоток тяговых электрических машин
тепловоза внесем в таблицу 3, а расчеты
произведем с помощью ПК.

Вывод:
после проведения проверки степени
нагревания электрических машин тепловоза
2ТЭ121, с поездом весом Q=4850
т по перегонам от станции «А» до «В»,
без остановки максимальный перегрев
составляет – 62,59+15=77,59оС,
что находится в пределах нормы, а, значит,
никаких дополнительных мер по охлаждению
или по облегчению веса поезда принимать
не нужно.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

• V0 — начальная скорость;
• A — ускорение (имеет постоянное значение);
• t — время движения.

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.

Средняя скорость

Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.

Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла

Рис. 6. Иллюстрация к примеру

Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.

Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).

Рис. 7. Средняя скорость

Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.

Рис. 8. Перемещение равно 0

На практике чаще всего используется понятие средней путевой скорости.

Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).

Рис. 9. Средняя путевая скорость

Существует еще одно определение средней скорости.

Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.

Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:

Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.

Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).

Рис. 10. Иллюстрация к задаче

Дано:Найти:

Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем

Средняя скорость равна:

Полный путь (

Путь подъема на склон равен:

Путь спуска со склона равен:

Время, за которое пройден полный путь, равно:

Ответ:

Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.

Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна Мгновенная скорость

Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).

Рис. 11. Спидометр автомобиля показывает мгновенную скорость

Существует еще одно определение мгновенной скорости.

Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).

Рис. 12. Мгновенная скорость

Для того чтобы лучше понять данное определение, рассмотрим пример.

Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.

Рис. 13. График зависимости проекции перемещения от времени

На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 14. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от

Рис. 15. График зависимости проекции перемещения от времени

Рассчитываем среднюю скорость на данном участке времени:

Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть

A

Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.

Направление мгновенной скорости совпадает с направлением перемещения тела.

Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).

Рис. 16. Направление мгновенной скорости

Коэффициент использования пробега (КИПр)

Определяет степень использования пробега автомобиля с грузом.

При работе автомобиля на линии различают пробеги: общий, с грузом, холостой и нулевой.

Общий пробег — это расстояние в километрах, проходимое автомобилем в течение рабочего дня.

Пробег с грузом является производительным пробегом.

Холостой пробег — это пробег автомобиля без груза между пунктами разгрузки и погрузки.Нулевой пробег — это пробег автомобиля от парка до пункта погрузки и с последнего пункта разгрузки до парка, а также проезды на заправку топливом.Коэффициент использования пробега определяют по формуле:

где: Sгp — пробег с грузом, км; Sо.пр — общий пробег автомобиля, км.

Пример. Общий пробег автомобиля за день составил 320 км, с грузом — 244 км. Определить КИПр.

Решение.

Величина коэффициента использования пробега зависит от размещения пунктов погрузки и разгрузки, характера грузопотоков и организации диспетчерской службы на линии. Водители-новаторы добиваются сокращения непроизводительных пробегов за счет перевозки попутных грузов. Например, при перевозке сахарной свеклы с поля на сахарный завод они используют обратные рейсы для перевозки на поля минеральных удобрений.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Высокоскоростные

Самыми быстрыми считаются высокоскоростные поезда. Они способны двигаться со скоростью 200−400 км/ч. Главная их особенность заключается в том, что они не могут передвигаться по обычным рельсам. Для них строят специальное полотно, способное выдержать большие нагрузки. Высокоскоростная магистраль появилась еще в 2000-х годах и продолжает активно развиваться. Сейчас самые быстрые составы курсируют из столицы в другие города, а также позволяют из России добраться в европейские города.

К примеру, самым известным высокоскоростным составом выступает «Сапсан», который курсирует между столицей и Санкт-Петербургом и позволяет преодолеть расстояние между этими городами в два раза быстрее. «Аллегро» является международным высокоскоростным поездом, так как курсирует из Северной столицы в Хельсинки.

Сейчас РЖД занимается возведением высокоскоростной магистрали, длина которой составляет около 1500 км. По ней смогут ездить поезда со скоростью около 400 км/ч. Она соединит Москву с Поволжьем и Сибирью. Курсировать состав будет двигаться из столицы через Казань в Екатеринбург. В перспективе запланировано строительство подобной магистрали из Москвы в Сочи.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

1. Справочный портал «Калькулятор».
2. Allcalc.
3. Fxyz.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Расстояния между грузопунктами

Вариант 10

Тема. Перевозка
лесоматериалов. Доска длинной 2,5 метров.КамАЗ-53212 10 тн.

Таблица
1

Таблица
1

А1	А2	АТП
Б1	10	8	11
Б2	12	6	11
Б3	16	16	15
Б4	4	12	5
АТП	1	8	—

• Схема
  перевозок
• Таблица 2
• Среднесуточный
  объём перевозок грузов по заявкам
• грузоотправителей
  и грузополучателей

Грузо-отправители	Грузо-получатели	Род груза	Способперевозки	γст	Количество тонн, Qсут
А1	Б2	лесоматериалы	пакетный	1	100
А1	Б3	1	160
А2	Б1	1	100
А3	Б3	1	60

Таблица 3

Маршруты
перевозок

Маршруты перевозок	Количество тонн за сутки
1. А1Б3 – Б3А1	160
2. А3Б3 – Б3А3	60
3. А2Б1 – Б1А1 – А1Б2 – Б2А2*	200

1. *
   На кольцевом маршруте выбрать
   первоначальный пункт погрузки
2. Таблица 4
3. Показатели
   работы подвижного состава

Наименование показателей, ед. изм.	Значение показателей
1. Плановое время в наряде, ч	9
2. Среднетехническая скорость, км/ч	28
3. Суточный коэффициент выпуска	0,81
4. Режим работы АТП, дн.	250

• 1
• 3) 4)

1. Проводим анализ кольцевого маршрута

l01
+ l02-
lх!; l01
+ l02-
lх!;

12+10-16=6; 10+10-0=20;

Полученное
наименьшее значение и является оптимальным
т.е. 6. Принимаем к расчету 3-ю схему.

2. Методика определения технико-эксплуатационных показателей

(ТЭП) работы
подвижного состава

Методика расчета
основывается на определении потребного
количества автомобилей, необходимого
для выполнения суточного объема
перевозок, учитывая производительность
конкретного автомобиля.

2.1. Определение тэп работы подвижного состава по каждому маршруту

1. Технико-эксплуатационные
   показатели рассчитываем по каждому
   заданному маршруту.
2. Время, затрачиваемое
   на оборот, определяется по формуле
3. tоб
   = (lм/Vт)
   + n·tп-р,
   ч, (1)

при механизированной
погрузку и разгрузке
tп-р=20
мин.=0,3 ч справочное пособие В.И. Савина

Скорость движения грузовых автомобилей

Добрый день, уважаемый читатель. В этой статье речь пойдет об ограничениях скорости движения грузовых автомобилей, предусмотренных правилами дорожного движения.

Сегодня Вы узнаете о том, что в большинстве случаев скорость грузовых автомобилей категорий C и CE несколько меньше, чем скорость легковых машин в аналогичных ситуациях.

Однако, как показывает практика, 99 процентов водителей грузовиков пересели на них с легковых машин, а десятый раздел ПДД перед этим открыть даже не удосужились. Поэтому и едут грузовики чаще всего со значительным превышением скорости.

Сегодня будут рассмотрены несколько групп грузовых автомобилей:

Обо всем по порядку.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Скорые

Техническая скорость скорых составов не отличается от пассажирских, но благодаря тому, что они делают мало остановок (только на крупных станциях и вокзалах) расстояние они преодолевают значительно быстрее. Маршрутная скорость таких поездов колеблется от 50 до 90 км/ч. Стоимость билета в немного дороже. На просторах государства ездят сотни таки поездов, причем в разных направлениях.

К примеру, поезд под названием «Сура» курсирует из Москвы в Пензу, а «Лотос» соединят столицу с Астраханью. Между Москвой и Челябинском курсирует также скорый поезд «Южный Урал». Существуют и другие поезда такого же типа на других маршрутах. Обычно они не имеют специального названия, а просто нумеруются. Скорые поезда отправляются из Москвы практически во все регионы.