Абсолютная и относительная погрешность — методы и алгоритмы вычислений

Погрешности измерения напряжения и тока

Классификация погрешности измерений

Виды измерений

Измерение тока и напряжения в электрической цепи проводят в диапазоне частот от 0 Гц до 1 ГГц. На более высоких частотах эти величины теряют свою однозначность в линии передачи и в её поперечном сечении. По этим причинам на сверхвысоких частотах предпочитают измерять мощность, а не ток и напряжение.

С точки зрения получения значения измеряемой величины по результатам первичных измерений различают прямые и непрямые (косвенные) измерения.

Прямое измерение – это измерение, при котором значение величины Х получают непосредственно по показанию соответствующего прибора Х_п без дополнительных расчетов Х= Х_п.

Примеры прямых измерений: измерение силы тока – амперметром, напряжения – вольтметром и т.д. При непрямом (косвенном) методе измерения величину Х определяют по результатам прямых измерений величин у₁, у ₂, … у _п, которые связаны с нею определенной функциональной зависимостью

Качество измерений тем выше, чем ближе результат измеренияХ_i к истинному значению Х. Абсолютная погрешность:

Количественной характеристикой качества измерения является погрешность измерения. Погрешность измерительных приборов отражает свойства только самого измерительного устройства, обусловленные структурными схемами, конструктивными особенностями приборов, применяемых в них материалов и элементов, технологии их изготовления, регулировки и градуировки. Следует различать погрешность измерительного прибора (инструментальная погрешность) и погрешность измерения прибором некоторого сигнала. Погрешность прибора – это часть погрешности измерения некоторого сигнала измерительным прибором, обусловленная неидеальностью (несовершенством) средств измерительной техники; она в определенной степени влияет на точность измерений. Погрешность прибора, определяемая по формуле (2.1), называется абсолютной. Более наглядное представление о точности измерений дает относительная погрешность прибора, которая рассчитывается по формуле (2.2).

Для сравнения приборов между собой введено понятие приведенная погрешность прибора

Х_кХ_ном

Если абсолютная погрешность прибора постоянна по всей шкале, то его относительная погрешность существенно увеличивается к началу шкалы. Поэтому целесообразно выбирать прибор (или шкалу прибора) с таким пределом измерения, при котором его указатель при измерении располагается ближе к концу шкалы.

Одной из характеристик прибора является класс точности. Класс точности прибора К_п определяет наибольшую (предельную) допустимую приведенную погрешность прибора в рабочей области шкалы, выраженную абсолютным числом, значение которого равно приведенной погрешности в процентах. По классу точности можно определить наибольшую абсолютную погрешность ∆, которую может иметь прибор в любой точке шкалы (без учета знака).

Например, при использовании вольтметра со шкалой 0 ÷ 100 В (Х_ном=100В) класса точности 1.5 на любой отметке его шкалы основная абсолютная погрешность не превышает значения

∆ ≤ ± К_п ∙ Х_ном / 100% = ± 1.5 ∙ 100 / 100% =± 1.5 В

При этом она может на отдельных отметках шкалы быть меньше 1.5 В или даже равна нулю. Приведенная погрешность соответствует максимальной относительной погрешности.

Класс точности электроизмерительного прибора устанавливают на заводе при калибровке по образцовому прибору в нормальных условиях. Нормальными условиями считаются температура окружающей среды (20 ± 5)˚С, относительная влажность (65 ± 15)%, атмосферное давление (100 000 ± 4 00) Па или (760 ± 30) мм рт. ст., напряжение питающей сети 220В ± 2% с частотой 50 Гц.

По зависимости погрешности от измеряемой величины Х различают аддитивные погрешности (независящие от Х), и мультипликативные (линейно зависящие от Х). Для аналоговых измерительных приборов с аддитивной погрешностью установлены такие классы точности:

К (%) = (1; 1,5; 2; 2,5; 4; 5; 6)∙10 n , где n = 1, 0, -1,-2.

В зависимости от места и причины возникновения различают такие основные составляющие погрешности от:

— несоответствия (неадекватности) модели измеряемого объекта его реальным свойствам и величине;

— упрощения математических моделей измерительных преобразований;

— взаимного влияния средств измерений и объекта;

— несовершенство средств измерений;

— влияния внешних факторов на объект и средства измерений;

— несовершенства вычислительного алгоритма и обработки результата наблюдения.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Точность

Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.

Распределение Гаусса

Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:

Здесь  — среднее значение, показывает дисперсию и соответствует RMS-значению шумового сигнала. Функция дает кривую распределения вероятностей, как показано на рисунке ниже, где среднее значение и эффективная амплитуда шума .

Распределение вероятностей с и

В таблице указаны шансы получения значений в заданных пределах.

Граница	Шанс
0.5·σ	38.3 %
0.674·σ	50.0 %
1·σ	68.3 %
2·σ	95.4 %
3·σ	99.7 %

Как видно, вероятность того, что измеренное значение лежит в диапазоне ± равна .

Повышение точности

Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Методики расчета

Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение

Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение

Полученное число умножают на 100%.

Для определения предельного отклонения выбирают наибольшее значение из всех полученных.

Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:

1. Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
2. Полученные результаты складывают между собой.
3. Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
4. Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.

Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения

Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение

При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.

При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

1. Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
2. Из этих величин выбирают минимальную и максимальную.
3. Вычисляют среднее значение Х.
4. В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
5. Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

а a изм аист ед.изм. 4

Это
размерная, положительная величина, характеризующая отклонение измеренного от
истинного значений.

Относительная погрешность – это
отношение абсолютной погрешности к истинному значению измеряемой величины.

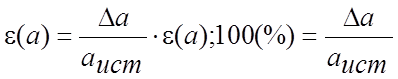                                                                     (5)

Относительная
погрешность (5) – безразмерная величина, она измеряется в долях или процентах и
показывает какую часть от истинного значения измеряемой величины составляет
погрешность.

На
практике вместо неизвестного истинного значения используют среднее значение
измеряемой величины.

Формула (5) позволяет по
известной одной из характеристик определить другую. Часто вначале удобнее найти
относительную, а через неё абсолютную.

Если
измерение выполнено и погрешности определены, то окончательный результат
записывается в виде

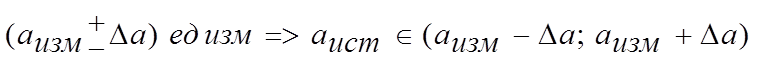        .                (6)

что эквивалентно заданию
интервала, в котором лежит истинное значение искомой величины. И чем уже данный
интервал, тем точнее измерения и наоборот.

4.
Вычисление погрешностей.

За
абсолютную погрешность однократно измеряемой величины применяют приборную
погрешность.

Для
простых измерительных и цифровых приборов приборная погрешностьравная
половине цены деления прибора.

                                         .                                                     (7)

Например:
приборная погрешность

                  
миллиметровой линейки (с=1 мм/_дел) равна, Δа_пр
=  0,5 мм.

                  
штангенциркуля (с=0,05 мм/_дел) – Δа_пр
= 0,025 мм.

                   эл.
секундомера (с=0,001 с/_дел) – Δа_пр
= 0,0005 с.

Для
стрелочных электроизмерительных приборов приборная погрешность определятся
через класс точности прибора (характеристика прибора указанная на его
шкале).

                                              ,                                               
(8)

представляющая
собой отношение приборной погрешности к максимальному значению измеряемой
прибором величины. Из (8) для приборной погрешности стрелочных
электроизмерительных приборов получаем:

                                
ΔАприб. = 0,01 · К · Аmax
.                  
                          (9) 

Часто
в расчетах приходится использовать физические и математические постоянные,
которые как правило выражаются сложными десятичными дробями

(π=
3.141593… , е = 2.718282… , с = 2.99792… · 108 м/_с

 q_e =
1,60219… · 10-19 Kл , m_е =
1.67265… · 10-31к2    и т.д.). 

При
использовании постоянных мы вынуждены их округлять т.е. брать приближённые
значения, это также даёт вклад в погрешность. К погрешностям табличных величин
относятся так же как и к приборным.

За
погрешность табличной величины принимают половину  единицы последнего разряда
табличной величины, выбранной с заданной точностью.

Например; при определении
плотности тела цилиндрической формы необходимо использовать число π.
Предварительно оговаривается точность расчётов (например вычисления проводят с
точностью до        

четырёх  значащих цифр).
Тогда используемое число π и погрешность Δπ соответственно будут равны:

π =
3.142,     Δπ = 0.0005

и окончательная запись числа
π с погрешностью имеет вид:

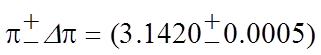
б)
Погрешности многократно измеряемых величин.

Погрешности
многократных измерений в рамках линейной теории оцениваются по следующей схеме

Погрешность

Погрешность является индикатором корректности измерения. Из-за того, что в одном измерении точность оказывает влияние на погрешность, то учитывается среднее серии измерений.

Погрешность измерительного прибора обычно задается двумя значениями: погрешностью показания и погрешностью по всей шкале. Эти две характеристики вместе определяют общую погрешность измерения. Эти значения погрешности измерения указываются в процентах или в ppm (parts per million, частей на миллион) относительно действуюшего национального стандарта. 1% соответствует 10000 ppm.

Погрешность приводится для указанных температурных диапазонов и для определенного периода времени после калибровки

Обратите внимание, что в разных диапазонах, возможны, и различные погрешности

Погрешность показаний

Указание процентного отклонения без дополнительной спецификации также относится к показанию. Допустимые отклонения делителей напряжения, точность усиления и абсолютные отклонения при считывании и оцифровке являются причинами этой погрешности.

Неточность показаний в 5% для значения 70 В

Вольтметр, который показывает 70.00 В и имеет спецификацию «± 5% от показаний», будет обладать погрешностью в ±3.5 В (5% от 70 В). Фактическое напряжение будет лежать между 66.5 и 73.5 вольтами.

Погрешность по всей шкале

Этот тип погрешности обусловлен ошибками смещения и ошибками линейности усилителей. Для приборов, которые оцифровывают сигналы, присутствует нелинейность преобразования и погрешности АЦП. Эта характеристика относится ко всему используемому диапазону измерений.

Вольтметр может иметь характеристику «3% шкалы». Если во время измерения выбран диапазон 100 В (равный полной шкале), то погрешность составляет 3% от 100 В = 3 В независимо от измеренного напряжения. Если показание в этом диапазоне 70 В, то реальное напряжение лежит между 67 и 73 вольтами.

Погрешность 3% шкалы в диапазоне 100 В

Из приведенного выше рисунка ясно, что этот тип допустимых отклонений не зависит от показаний. При показании 0 В реальное напряжение лежит между -3 и 3 вольтами.

Погрешность шкалы в цифрах

Часто для цифровых мультиметров приводится погрешность шкалы в разрядах вместо процентного значения.

У цифрового мультиметра с 3½ разрядным дисплеем (диапазон от -1999 до 1999), в спецификации может быть указано «+ 2 цифры». Это означает, что погрешность показания 2 единицы. Например: если выбирается диапазон 20 вольт (± 19.99), то погрешность шкалы составляет ±0.02 В. На дисплее отображается значение 10.00, а фактическое значение будет между 9.98 и 10.02 вольтами.

Вычисление погрешности измерения

Спецификации допустимых отклонений показания и шкалы вместе определяют полную погрешность измерения прибора. Ниже при расчете используются те же значения, что и в приведенных выше примерах:

Точность: ±5% показания (3% шкалы)

Диапазон: 100 В

Показание: 70 В

Полная погрешность измерения вычисляется следующим образом:

В этом случае, полная погрешность ±6.5В. Истинное значение лежит между 63.5 и 76.5 вольтами. На рисунке ниже это показано графически.

Полная неточность для неточностей показания 5% и 3% шкалы для диапазона 100 В и показания 70 В

Процентная погрешность — это отношение погрешности к показанию. Для нашего случая:

Цифры

Цифровые мультиметры могут иметь спецификацию «± 2.0% показания, + 4 цифры». Это означает, что 4 цифры должны быть добавлены к 2% погрешности показания. В качестве примера снова рассмотрим 3½ разрядный цифровой индикатор. Он показывает 5.00 В для выбранного диапазона 20 В. 2% показания будет означать погрешность в 0,1 В. Добавьте к этому численную погрешность  (= 0,04 В). Общая погрешность, следовательно, 0,14 В. Истинное значение должно быть в диапазоне между 4.86 и 5,14 вольтами.