Формула жесткости пружины

Жёсткость деформируемых тел при их соединении

При соединении нескольких упруго деформируемых тел (далее для краткости — пружин) общая жёсткость системы будет меняться. При параллельном соединении жёсткость увеличивается, при последовательном — уменьшается.

Параллельное соединение

При параллельном соединении пружин с жёсткостями, равными жёсткость системы равна сумме жёсткостей, то есть

В параллельном соединении имеется пружин с жёсткостями К ним прикладывается сила При этом к пружине 1 прикладывается сила к пружине 2 сила … , к пружине сила

Из III закона Ньютона,

Теперь из закона Гука выведем: Подставим эти выражения в равенство (1): сократив на получим: что и требовалось доказать.

Последовательное соединенение

При последовательном соединении пружин с жёсткостями, равными общая жёсткость равна единице, делённой на сумму обратных величин жёсткостей, то есть

В последовательном соединении имеется пружин с жёсткостями Из закона Гука следует, что Сумма удлинений каждой пружины равна общему удлинению всего соединения

На каждую пружину действует одна и та же сила Согласно закону Гука, Из предыдущих выражений выведем: Подставив эти выражения в (2) и разделив на получаем что и требовалось доказать.

Сила Архимеда

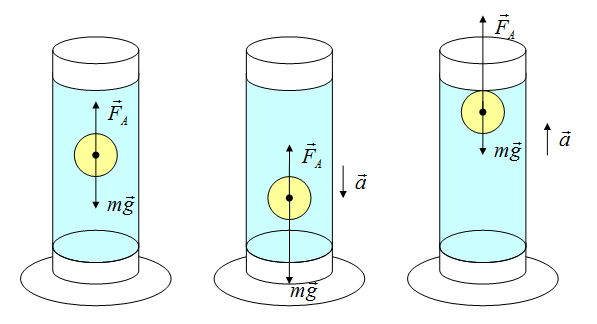
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как Сила Кулона, сила Ампера, сила Лоренца.

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Локальная система отсчёта

— это система отсчёта, которая может считаться инерциальной, но лишь в бесконечно малой окрестности какой-то одной точки пространства-времени, или лишь вдоль какой-то одной незамкнутой мировой линии.

Преобразования Галилея. Принцип относительности в классической механике.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система Kбудет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+vt;y=y’;z=z’;t=t’, названных преобразованиями Галилея.Механический принцип относительности.Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.Нарушение классического закона сложения скоростей.Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x’=(x-vt)/(1-v 2 /c 2 ); y’=y; z’=z; t’=(t-vx/c 2 )/(1-v 2 /c 2 ). Эти преобразования называются преобразованиями Лоуренса.

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Расчет стальных канатов. Формула. Нормы отбраковки канатов.

Стальные канаты согласно Госгортехнадзору, рассчитываются по формуле:

S = PK,

Где

S – самое большое усилие на канат, кг;

P – разрывное усилие каната, кг;

K – табличный коэффициент запаса прочности, выбирается из таблицы 1. (для грузовых и тяговых канатов, а также оттяжек (расчалок).

Когда проверяют канаты на прочность, их разрывное усилие берется из сертификата, а в случае его отсутствия определяется практически, путем лабораторного испытания. В этом случае расчет каната ведется по суммарному усилию разрыва отдельных проволок, умноженному на 0,83.

Размеры барабанов для каната.

Самый меньший диаметр барабана или блока, который допускается огибать стальным канатом рассчитывается по формуле:

D ≥ d(с – 1),

Где

D – наименьший диаметр канавки огибаемого барабана или блока, мм;

d – диаметр каната, мм;

e – коэффициент, который зависит от типа грузоподъемной машины и режима её работы. (выбирается по таблице 2. см. ниже)

Диаметр уравнительного блока нужно принимать на 40% меньше диаметра барабанов и блоков.

Более детально про виды, типы свивок, вес стальных канатов Вы можете узнать в статье: Характеристики стальных канатов. Канат двойной свивки типа ТК, ЛК-Р.

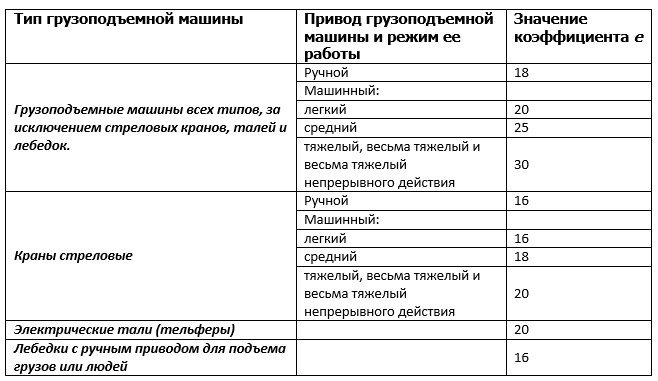
Таблица 1.

Наименьшие допустимые значения коэффициентов запаса прочности К.

Уход за стальными канатами. Смазка канатов.

Нельзя допускать резких переломов, «жучков», сплющивания каната из-за падения предметов или защемления его. Необходимо постоянно смазывать канаты специальной мазью не содержащей влаги, это мази с таким составом по весу:

• — масляный гудрон — 68%;
• — битум марки 3 — 10%;
• — канифоль – 10%;
• — технический вазелин – 7%;
• — графит – 3%;
• — озокерит – 2%.

Также возможно смазывать стальные канаты вязким минеральным маслом по типу вискозина.

Периодичность смазки стальных канатов.

Период смазки зависит от того находится он в работе или просто хранится на складе:

• — при работе – через каждые 1,5 месяца;
• — при хранении на складе – через 6 месяцев.

Расход смазки.

Расход смазки зависит от того новый канат или б/у. Если канат новый, то расход составляет 0,3 кг на 100 п.м. каната, а если б/у – 0,45 кг на 100 п.м. каната.

Идеально было бы не допускать канаты трению о кирпичные здания и металлоконструкции, соприкосновения их с электросварочными проводами.

Хранить желательно в сухих, закрытых помещения, хорошо смазанными (с периодичностью смазки описанной выше), в бухтах и на деревянном настиле.

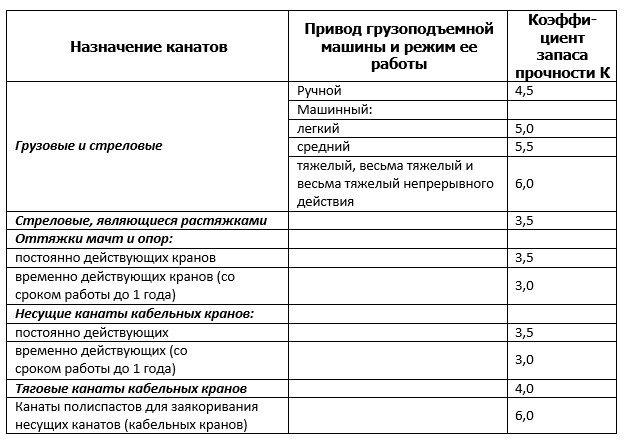
Таблица 2.

Наименьшие допустимые коэффициенты запаса прочности e.

Выбраковка стальных канатов.

В таблице 3 приведены данные согласно которым происходит отбраковка грузовых канатов по количеству обрывов проволок. При подсчете обрыв толстой проволоки принимается за 1.7, а тонкой — за 1.0. В табл. 3 приведены значения для трех типов каната 6 × 19 = 114, 6 × 37 = 222, 6 × 61 = 366. Если необходимо подсчитать отбраковку каната, которого нет в табл. 3, то данные этой таблицы нужно умножить на отношение числа проволок в наружных слоях прядей искомого каната и ближайшее значение по табл. 3. Это число берется самое близкое по количеству проволок и прядей в сечении.

К дальнейшей работе канат не допускается, если обнаружилась оборванная пряжа.

Таблица 3.

Нормы отбраковки грузовых канатов.

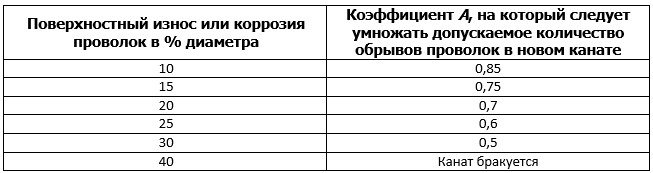
Таблица 4.

Коэффициент уменьшения допускаемого числа обрывов проволок при наличии поверхностного износа и коррозии проволок каната.

Как определить жесткость пружины

Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

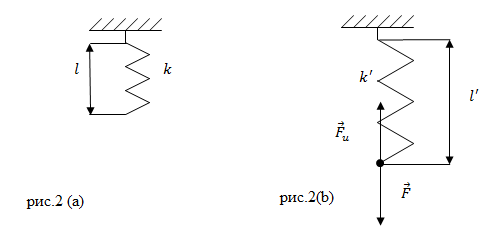
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:

При упругих деформациях выполняется закон Гука:

Из (1.2) найдем удлинение пружины:

Длина растянутой пружины равна:

Вычислим новую длину пружины:

Ответ. 1) $k’=10 frac$; 2) $l’=0,21$ м

Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?

Решение. Если пружины соединены последовательно, то деформирующая сила ($overline$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:

Для второй пружины запишем:

Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:

Из равенства (2.3) получим удлинение первой пружины:

Ответ. $Delta l_1=frac$

Основные характеристики

Независимо от вида пружин, особенности их работы, связанные с постоянно деформацией, требуют наличия таких параметров:

• Способности сохранять постоянное значение упругости в течение заданного срока.
• Пластичности.
• Релаксационной стойкости, благодаря которой деформации не становятся необратимыми.
• Прочности, то есть способности выдерживать различные виды нагрузок: статические, динамические, ударные.

Каждая из этих характеристик важна, однако при выборе упругой комплектующей для конкретной работы в первую очередь интересуются ее жесткостью как важным показателем того, подойдет ли она для этого дела и насколько долго будет работать.

Свойства пружин подвески

Когда торсионы на транспортных средствах заменили на пружины, улучшилась управляемость, подвески стало удобнее обслуживать. Пружины поддерживают клиренс автомобиля, уменьшая вибрации и удары во время движения транспортного средства.

Чтобы езда была комфортной, необходимо правильно подобрать детали. Если теххарактеристики будут неподходящими, то положительные свойства подвески будут сведены к нулю

Потому важно учитывать следующие параметры:

• диаметр — его увеличение влияет на жёсткость;
• количество витков — при увеличении жёсткость снижается;
• форма.

Зачастую автовладельцы стремятся установить в подвеску более жёсткие детали. Это способствует увеличению чувствительности рулевого колеса к управлению водителем, но сцепление с дорогой ухудшается.

Любители спортивного стиля езды считают, что, напротив, лучше ставить детали с пониженной жёсткостью. Однако такая подвеска может создать проблемы на просёлочных дорогах.

Давайте рассмотрим подробнее, какие пружины лучше установить на ВАЗ.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Основные методы крепления пружин

При проведении расчетов уделяется внимание тому, каким образом проводится соединение пружин. Этот момент оказывает влияние на следующее:

1. Жесткость системы. Этот показатель встречается практически во всех проводимых расчетах при последовательном подключении деталей. Зависит он от самых различных моментов, к примеру, коэффициента жесткости каждого.
2. Требуемое усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто по причине того, что может обеспечивает накопление кинетической энергии.
3. Размер кинетической и потенциальной энергии. После того как изделие было выведено из положения равновесия начинает накапливаться кинетическая энергия. При этом она сохраняется на протяжении всего периода, пока к телу приложено усилие.
4. Вероятность возникновения свободного колебательного движения, а также степень сопротивления подобному явлению. Для расчетов колебательного движения также применяются специальные формулы.

Они характеризуются довольно большим количеством особенностей

Прежде чем рассматривать применение подобных способов соединения следует уделить внимание особенностям самого изделия:

1. Деталь изготавливается из проволоки, которая получается методом проката. Она обладает высоким показателем упругости, а также устойчивостью к воздействию окружающей среды.
2. Прокат изготавливают из специального сплава, способного выдерживать периодическую деформацию. Под заказ может производится деталь из обычных углеродистых сплавов или легированных металлов, все зависит от конкретного случая.
3. Проволока накручивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
4. Выделяют два основных типа детали: растяжения и сжатия. Первый вариант исполнения характеризуется тем, что витки находятся практически вплотную. В случае изготовления изделия для сжатия выдерживается определенный зазор, который позволяет кольцам сближаться, а самому изделию сжиматься.
5. Характеризуется изделие самыми различными показателями. Примером можно назвать диаметр проволоки, созданных колец из нее, шаг расположения витков. Все эти параметры указываются в технической документации.

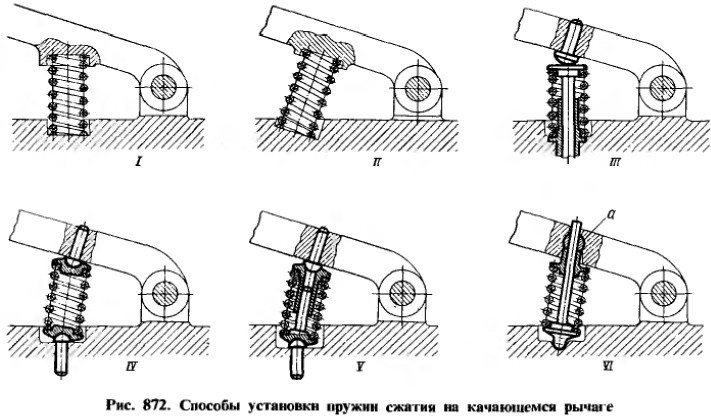
Сегодня они встречаются практически повсеместно. Это связано с тем, что подобное изделие практически незаменимо в случае, когда требуется возвратно-поступательное движение.

Класс «А» и «В» – существенны ли отличия

Для многих автолюбителей жесткость пружин по цветам равносильна жесткости по классам. Класс «А», независимо от цвета, более жесткий, нежели класс «В». На самом деле это не совсем верное утверждение. Класс «А» действительно больше подходит для автомобилей, которые часто эксплуатируются с высокой нагрузкой. Но разница здесь совсем невелика – порядка 25 кг. Несмотря на обязательное нанесение маркировки, до сих пор встречаются образцы, на которых она отсутствует. В таком случае, даже если цветовая маркировка элементов идентична, от их покупки и использования лучше отказаться.

Многими автомобилистами недооценивается значение качественных пружин, особенно при интенсивной эксплуатации автомобиля. Пружины не зря имеют маркировку по цветам – так гораздо проще сориентироваться начинающему водителю, который впервые занимается собственноручной заменой этого элемента. Приобретение изделий надлежащего качества, пусть и по более высокой цене, неизбежно окупится более мягкой ездой, меньшим износом автомобиля, а также меньшими нагрузками на самого водителя. Научно доказано, что высокие вибрационные нагрузки на человека приводят к быстрой утомляемости и снижению концентрации при движении.

Жесткость пружины. Как рассчитать.

Измерение параметров жесткости пружин разных типов

При производстве на предприятии и для применения необходимо определить способность пружины выдерживать определенные типы нагрузок. Для этого высчитывается т.н. коэффициент Гука – обозначение жесткости пружины, от которого зависит её надёжность. На этот параметр влияет материал, выбранный для изготовления. Это может быть сталь, легированная кремнием, ванадием, марганцем, другими добавками. Также применяются нержавейка, бериллиевая и кремнемарганцевая бронза, сплавы на основе никеля и титана. Если деталь выпускается для применения при высоких нагрузках, экстремальных температурах, используются специальные марки легированной стали. Нижегородская метизная корпорация имеет возможность производить пружины под заказ, создавая изделия с заданными характеристиками.

Что такое жесткость?

Говоря о практике, а не физических терминах, это сила, приложив которую, можно сжать пружину. Если вы знаете прилагаемое усилие, можно определить, какой будет деформация, и наоборот. Это существенно облегчает вычисления.

Коэффициент высчитывается для пружин кручения, растяжения, изгиба, сжатия – всех наиболее популярных в промышленности разновидностей этого изделия. Также следует отметить два основных типа:

• С линейной (постоянной) жесткостью;
• С прогрессивной (зависящей от положения витков) жесткостью.

Часто производитель наносит на готовую продукцию пометку краской. Если такого обозначения нет, применяется формула определения жесткости пружины через массу и длину, упрощающая задачу. Она изначально разрабатывалась для пружин растяжения, была получена методом измерения соответствия массы грузы с изменениями геометрии.

Также данный параметр может быть прогрессирующим – растущим — или регрессирующим – убывающим. Во втором случае параметр «жесткости» принято называть «мягкостью». В отдельных механизмах, например, в автомобилестроении, этот параметр особенно актуален.

Какие вводные данные требуются?

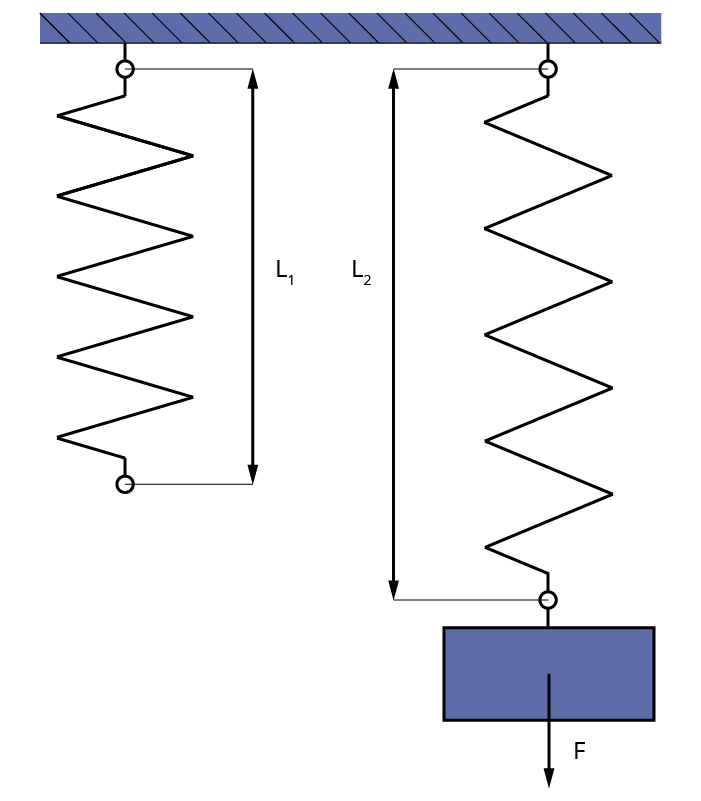
При расчёте важно знать следующую информацию:

• Из какого материала выполнено изделие;
• Точный диаметр витков – Dw ;
• Общий диаметр самой пружины – Dm ;
• Количество витков – Na .

Таким образом, к коэффициенту жесткости пружинного механизма может применяться формула:

k=G*(Dw)^4/8 * Na * (Dm)^3

Переменная G

означает модуль сдвига. Это значение можно найти в таблицах для разных материалов. К примеру, у пружинной сталиG=78,5 ГПа .

Далее разберемся, как определить жесткость пружины по формуле:

k=F/L.

Длина L

бывает двух типов:

• L1 – измеренная в вертикальном положении без груза;
• L2 – полученная при подвешивании груза с точно известной массой.

Например, 100

-граммовая гиря, закреплённая в нижней части, воздействует с силойF , равной1 Н . Получаем разницу между двумя показателями длины:

L = L2 – L1

При этом следует уточнить, что степень жесткости не определяет распрямление в исходное состояние. На него воздействуют сразу несколько факторов.

Насколько важен показатель, и на что он влияет?

Характеристики пружины важны не только для соответствия ГОСТам и проведения сертификации. Они влияют на сроки эксплуатации изделий, в которых используются, а это огромное количество приборов, деталей, механизмов, от мебели, до различных транспортных средств.

Поэтому данная величина напрямую влияет на надёжность готовых изделий, оборудования, техники, в которых используются элементы, содержащие пружины.

Часто люди интересуются, как рассчитать жесткость пружины цилиндрической винтовой. Для таких случаев учитывается не только модуль сдвига, но и параметр Rs

– напряжение, допускаемое при кручении. Здесь в расчёт берётся тип материала, его физические свойства, механические характеристики.

Следующий вопрос – в чем измеряется коэффициент жесткости пружины при расчётах. Традиционно в системе измерений, принятой в нашей стране принято записывать значение в Н/м

– ньютонах на один метр. Также это значение в качестве альтернативного варианта может записываться в килограммах на квадратный сантиметр, дин/см, граммах на квадратный сантиметр (расчёты в системе СГС).

Отличия пружин подвески и их маркировка

Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:

1. изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
2. изготавливать пружины одинаковой высоты, но различной жесткости;
3. изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.

Статья в тему: Как зарегистрироваться на экзамен в ГИБДД через госуслуги? Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.

Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.

• Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
• Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.

Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.

Статья в тему: Самостоятельное приготовление электролита для АКБ